Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

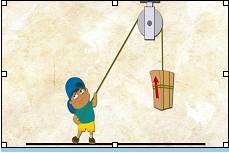
a) Biểu diễn lực căng dây:
Lực căng dây là lực mà dây kéo lên gói hàng để duy trì nó ở vị trí cao. Theo nguyên lý Newton thứ ba, lực căng dây có cùng độ lớn nhưng ngược chiều với lực trọng trên gói hàng. Vì vậy, lực căng dây có độ lớn là 150N và hướng lực là ngược chiều với hướng lực trọng.
b) Lực tác dụng của cậu bé:
Để giữ gói hàng đứng yên trên cao, cậu bé phải tạo ra một lực tác dụng lên gói hàng có độ lớn bằng đúng lực trọng của gói hàng. Vì vậy, lực tác dụng của cậu bé cần có độ lớn là 150N và hướng lực cần phải trùng với hướng lực trọng.

Chọn hệ trục tọa độ Oxy như hình vẽ. Gọi \(\overrightarrow{F_k}\) là lực kéo tác dụng lên sợi dây, \(\overrightarrow{P}\) và \(\overrightarrow{N}\) lần lượt là trọng lực tác dụng lên vật. Ta phân tích \(\overrightarrow{F_k}\) thành 2 lực \(\overrightarrow{F_{k_x}}\) và \(\overrightarrow{F_{k_y}}\) trên các trục Ox, Oy.
a) Công của lực kéo là \(A_k=F_k.s.cos\left(\overrightarrow{F_k},\overrightarrow{s}\right)=100.20.cos45^o=1000\sqrt{2}\left(J\right)\)
b) Gọi \(\overrightarrow{F_{ms}}\) là lực ma sát tác dụng lên vật. Chọn chiều dương là chiều chuyển động của vật
Áp dụng định luật II Newton:
\(\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\) (1)
Chiếu (1) lên Oy: \(N=P-F_{k_y}=400-F_k.sin45^o=400-175\sqrt{2}\left(N\right)\)
Do đề bài không nói gì về loại chuyển động của vật nên mình sẽ xem đây là chuyển động nhanh dần đều nhé. Khi đó, ta sẽ có \(s=\dfrac{1}{2}at^2\Rightarrow20=\dfrac{1}{2}a.180^2\) \(\Rightarrow a=\dfrac{1}{810}\left(m/s^2\right)\).
Chiếu (1) lên Ox, ta được \(F_{k_x}-F_{ms}=m.a\Rightarrow F_{ms}=F_{k_x}-m.a=350.cos45^o-400.\dfrac{1}{180}\)\(=170\sqrt{2}-\dfrac{20}{9}\) (N)
\(\Rightarrow A_{ms}=-\left(170\sqrt{2}-\dfrac{20}{9}\right).20\approx-4763,88\left(J\right)\)

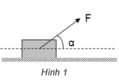
a) Vẽ hình , biểu diễn đúng các lực tác dụng lên vật
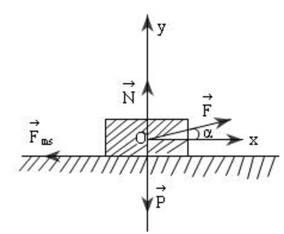
Phương trình định luật II Niu-tơn đối với vật là:
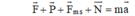
b) Chiếu (1) lên Oxy ta được:
Ox: F. cos a - F ms = m.a
Oy: F sina + N - P = 0.
Từ đó rút ra 
Từ (2) : Đk để mMax 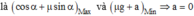
Theo bất đẳng thức Bunhiacopxki:
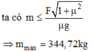
Dấu = xảy ra khi 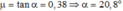

\(F_k-F_{ms}=m.a\Leftrightarrow a=\dfrac{F_k-F_{ms}}{m}=...\left(m/s^2\right)\)
\(v=v_0+at=\dfrac{F_k-F_{ms}}{m}.3=...\left(m/s\right)\)
\(F_{ms}=-m.a'\Rightarrow a'=-\dfrac{F_{ms}}{m}=...\left(m/s^2\right)\)
\(v'^2-v_0'^2=2a'S\Leftrightarrow v_0'=-\sqrt{2.a'.1}=...\left(m/s\right)\)
\(S=v_0't+\dfrac{1}{2}a't^2\Leftrightarrow1=-\sqrt{2a'}.t+\dfrac{1}{2}a't^2\Rightarrow t=...\left(s\right)\)
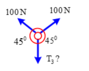
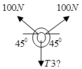
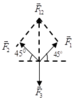
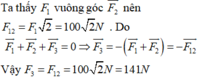

Chọn đáp án C
? Lời giải: