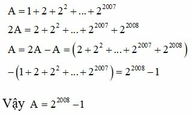Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt A=1+2+22+...+220081+2+22+...+22008
=>2A=2.(1+2+22+...+220081+2+22+...+22008)
=>2A=2+22+23+...+220092+22+23+...+22009
=>2A-A=(2+22+23+...+220092+22+23+...+22009)-(1+2+22+...+220081+2+22+...+22008)
=>A=22009−122009−1
=>A=(-1).(−2)2009(−2)2009+(-1).1
=>A=(-1).[(−2)2009+1][(−2)2009+1]
=>A=(-1).(1−22009)(1−22009)
=>1+2+22+...+220081+2+22+...+22008/1-2200922009
=(−1).(1−22009)1−22009(−1).(1−22009)1−22009=-1
Giải:
Đặt A=1+2+22+23+...+22008
2A=2+22+23+24+...+22009
2A-A=(1+2+22+23+...+22008)-(2+22+23+24+...+22009)
A =1-22009
Vậy B=1-22009/1-22009=1
Chúc bạn học tốt!

Ta gọi tử của phân số B là A ta có:
A=1+2+2^2+2^3+...+2^2008
2A=2 + 2^2 + 2^3 + 2^4 +... + 2^2009
=>A=2^2009 - 1
A=-1 + 2^2009
ta thấy tử là số đối của mẫu =>B=\(\dfrac{-1}{1}\)

\(\left(\frac{1}{1.2.3}+\frac{1}{2.3.4}+....+\frac{1}{8.9.10}\right).x=\frac{23}{45}\)
\(\Leftrightarrow\left[\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+....+\frac{1}{8.9}-\frac{1}{9.10}\right)\right]x=\frac{23}{45}\)
\(\Leftrightarrow\left[\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{9.10}\right)\right].x=\frac{23}{45}\)
\(\Leftrightarrow\left(\frac{1}{2}.\frac{44}{90}\right).x=\frac{23}{45}\)
\(\Leftrightarrow\frac{11}{45}.x=\frac{23}{45}\Rightarrow x=\frac{23}{45}:\frac{11}{45}=\frac{23}{11}\)
nhung sao banj khong phan h ra ro rang,chang nhe den do khong phan h duoc sao

A = 1 + 2 + 2 2 + . . . + 2 2007
2 A = 2 + 2 2 + . . . + 2 2007 + 2 2008
A = 2A - A = ( 2 + 2 2 + . . . + 2 2007 + 2 2008 ) - ( 1 + 2 + 2 2 + . . . + 2 2007 ) = 2 2008 - 1
Vậy A = 2 2008 - 1

1.2(x-1)+(x-2)=x-4
2x-2+x-2=x-4
2x+ x-x=2+2-4
2x=0
=> x=0
Vậy x=0

Tính tổng 1-2+3-4+4-5+... 99-100 = ?
Ta có : 1-2+3-4+4-5+... 99-100 =
(1+3+5+ ...99) - (2+4+ ... 100) =
(1+99)x25 - (2+100)x25 = - 50
( từ 1 -> 99 có 50 số lẻ liên tiếp nên có 25 cặp số lẻ )
( từ 2 -> 100 có 50 số chẵn liên tiếp nên có 25 cặp số chẵn)
Hoặc
Áp dụng cấp số cộng : S = n1+n2+n3+... n = (n1+n).n/2
Ta có: (1+99)x25 - (2+100)x25 = -50
Tick nha

Ta có : \(\left(x+1\right)+\left(x+2\right)+\left(x+3\right)+...+\left(x+1000\right)=5750\)
\(\Leftrightarrow1000x+\left(1+2+...+1000\right)=5750\)
\(\Leftrightarrow1000x+\frac{1001.1000}{2}=5750\)
\(\Leftrightarrow1000x=\frac{5750}{500500}=\frac{23}{2002}\)
\(\Leftrightarrow x=\frac{23}{2002000}\)
(x+1)+(x+2)+...+(x+1000)=5750
=>x.1000+(1+2+3+...+1000)=5750
=>x.1000+[(1000+1).1000:2]=5750
=>1000x+(1001000:2)=5750
=>1000x+500500=5750
=>1000x=5750-500500=-494750
=>x=-494750:1000=-494,75
Có lẽ đúng >: ko chắc :P