Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi x và y lần lượt là số gam đồng và kẽm có trong vật đó
(Điều kiện: x, y > 0; x < 124, y < 124 )
Vì khối lượng của vật là 124g nên ta có phương trình x + y = 124
Thể tích của x (g) đồng là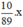 
(
c
m
3
)
Thể tích của y (g) kẽm là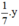 
(
c
m
3
).
Vật có thể tích 15cm3 nên ta có phương trình: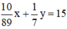 
Ta có hệ phương trình:
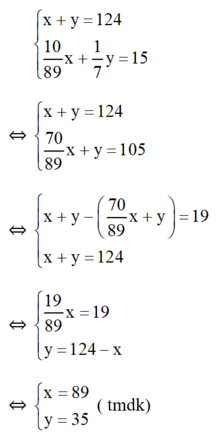
Vậy có 89 gam đồng và 35 gam kẽm.
Gọi x và y lần lượt là số gam đồng và kẽm có trong vật đó
(Điều kiện: x, y > 0; x < 124, y < 124 )
Vì khối lượng của vật là 124g nên ta có phương trình x + y = 124
Thể tích của x (g) đồng là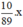 
(cm3)
Thể tích của y (g) kẽm là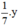 
(cm3).
Vật có thể tích 15cm3 nên ta có phương trình: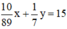 
Ta có hệ phương trình:
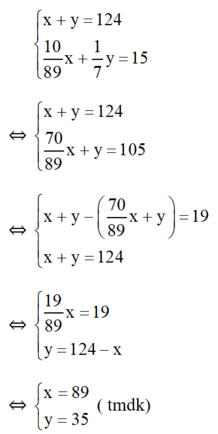
Vậy có 89 gam đồng và 35 gam kẽm.
Gọi khối lượng đồng trong hợp kim là x (0 < x < 124)
Ta có khối lượng kẽm trong hợp kim là 124 – x
Vì 89g đồng thì có thể tích là 10 c m 3 nên x (g) đồng có thể tích là 10x/89
7g kẽm thì có thể tích là 1 c m 3 nên 124 – x (g) kẽm có thể tích là (124-x)/7
Vì thể tích của hợp kim ban đầu là 15 c m 3 nên ta có phương trình:
10 x 89 + 124 - x 7 = 15 ⇔ −19x = −1691 ⇔ x = 89 (tmdk)
Vậy khối lượng đồng và kẽm trong hợp kim lần lượt là 89g và 35g
Đáp án: D
Tổng số học sinh dự thi của hai trường là: 396 : 88%=450 (HS)
Gọi số HS trường A là: x (HS) (x thuộc N*)
Số HS trường B dự thi là: 450-x
Số HS thi đỗ của trường A là: 85% x
Số HS thi đỗ của trường B là: 90%(450-x)
Theo đề bài ta có PT :
85% x +90%(450-x) = 396 <=> x = 180
=> Số HS dự thi trường B là: 450-180 = 270 ( HS)
Vậy số HS dự thi vào lớp 10 của trường A và B lần lượt là 180 và 270
Gọi x,y lần lượt số sinh lần lượt của trường THCS A và THCS B (x,y>0) (Học sinh)
Vì tổng số học sinh là 500: x+y=500 (1)
Mặt khác, với các thông tin về số học sinh đỗ, ta có hpt:
90% x + 80% y = 84%. 500
<=> 0,9x + 0,8y = 420 (2)
Từ (1), (2) ta có hpt:
\(\left\{{}\begin{matrix}x+y=500\\0,9x+0,8y=420\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=200\left(TM\right)\\y=300\left(TM\right)\end{matrix}\right.\)
Trường THCS A có số học sinh đỗ là: 200 x 90%= 180 (học sinh)
Số học sinh đỗ vào 10 của trường THCS B là: 300 x 80%= 240(học sinh)
Tổng số h/s dự thi của cả 2 trường là 420:84%=500 (h/s)
Gọi số h/s dự thi của trường A và B lần lượt là a,b (h/s) (a,b nguyên dương và 0<a,b<500)
=> a+b=500
Tỉ lệ đỗ của trường A là 80% nên số h/s thi đỗ của trường A là 80%.a=8/10.a
Tương tự số h/s thi đỗ của trường B là 9/10.b
Mà 2 trường có 420 h/s đỗ => 8/10.a+9/10.b=420
Giải hệ \(\hept{\begin{cases}a+b=500\\\frac{8}{10}a+\frac{9}{10}b=420\end{cases}}\)được a=300,b=200
gọi số hs thi trg A là x (hs) (x,y thuộc N*)
số hs thi trg B là y(hs)
tổng số hs 2 trg A và B là:
\(x+y=840:84\%=1000\left(1\right)\)
tổng số hs đỗ vào trg công lập của trg A và B là:
\(80\%x+90\%y=840\\ \Leftrightarrow0,8x+0,9y=840\left(2\right)\)
từ (1) và (2) => hpt:
\(\left\{{}\begin{matrix}x+y=1000\\0,8x+0,9y=840\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=400\\x=600\end{matrix}\right.\)
vậy.... pt r tự giải chi tiết ra nhá ~~ a lười bấm máy tính cho nhanh
Gọi x là số học sinh dự thi vào lớp 10 của trường A (h/s, \(x\in N\), \(0< x< 435\))
y là số học sinh dự thi vào lớp 10 của trường B (h/s, \(y\in N\), \(0< y< 435\))
Vì hai trường A và B có 435 học sinh dự thi nên ta có PT: \(x+y=435\) (1)
Vì trường A có tỉ lệ thi đỗ vào lớp 10 là 85%, trường B có tỉ lệ thi đỗ vào lớp 10 là 90%, và cả hai trường có tỉ lệ thi đỗ vào lớp 10 là 87% nên ta có PT: \(85\%x+90\%y=87\%\cdot435\) (2)
Từ (1) và (2), ta có HPT: \(\hept{\begin{cases}x+y=435\\85\%x+90\%y=87\%\cdot435\end{cases}}\)
Giải HPT, ta có: \(\hept{\begin{cases}x=261\\y=174\end{cases}}\) (TMĐK)
Vậy trường A có 261 học sinh dự thi và trường B có 174 học sinh dự thi, vào lớp 10.
Gọi x là số học sinh dự thi vào lớp 10 của trường A (h/s, \(x\in N\),\(0< x< 500\))
y là số học sinh dự thi vào lớp 10 của trường B (h/s, \(y\in N\),\(0< y< 500\))
Vì cả hai trường có 435 thi đỗ vào lớp 10 đạt tỉ lệ là 87% nên ta có PT: \(x+y=\frac{435}{87\%}\) <=> \(x+y=500\) (1)
Vì trường A có tỉ lệ thi đỗ vào lớp 10 là 85%, trường B có tỉ lệ thi đỗ vào lớp 10 là 90%, và cả hai trường có 435 học sinh thi đỗ vào lớp 10 nên ta có PT: \(85\%x+90\%y=435\) (2)
Từ (1) và (2), ta có HPT: \(\hept{\begin{cases}x+y=500\\85\%x+90\%y=435\end{cases}}\)
Giải HPT, ta có: \(\hept{\begin{cases}x=300\\y=200\end{cases}}\) (TMĐK)
Vậy trường A có 300 học sinh dự thi và trường B có 200 học sinh dự thi, vào lớp 10.