K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TC
28 tháng 10 2018
Tam giác ABC có MN // BC (M thuộc AB, N thuộc AC)
S(ACM)/S(ABC) = AM/AB (1)
S(ABN)/S(ABC) = AN/AC (2)
Mà S(ACM) = S(AMN) + S(CMN) (3)
và S(ABN) = S(AMN) + SBMN) (4)
Mặt khác do MNCB hình thang nên dễ dàng chứng minh
S(CMN) = S(BMN) (5)
Từ (3) , (4) và (5) cho:
S(ACM) = S(ABN) (6)
(1) , (2) và (6) cho:
AM/AB = AN/AC (đpcm)
-----------
Cách viết S(ABC) đọc là diện tích tam giác ABC
HT
3
8 tháng 6 2016
x1^2 -x2^2 = (x1 -x2).(x1+x2)
Sau đó bạn dùng viet thay vào pt trên r tính. Thực ra cái này nó phải tuỳ thuộc vào đề bài bạn ạ :)
9 tháng 6 2016
\(X_1^2-X_2^2=\left(X_1+X_2\right).\left(X_1-X_2\right)=\left(X_1+X_2\right).\sqrt{\left(X_1-X_2\right)^2}.\)
\(=\left(X_1+X_2\right).\sqrt{\left(X_1+X_2\right)^2-4X_1.X_2}\)
A
27 tháng 3 2019
Ta có: \(\sqrt{a^2}\ge0\Rightarrow\left(\sqrt{a^2}\right)^2=a^2\)
\(|a|\ge0\Rightarrow\left(|a|\right)^2=a^2\)
\(\Rightarrow\sqrt{a^2}=|a|,\forall a\in R\)
áp dụng \(A=\sqrt{\left(\sqrt{7-2}\right)^2}+\sqrt{\left(\sqrt{7-3}\right)^2}=|\sqrt{7}-2|+|\sqrt{7}-3|\)
\(=\sqrt{7}-2+3-\sqrt{7}=1\)
PT
1
PT
1
CM
24 tháng 12 2018
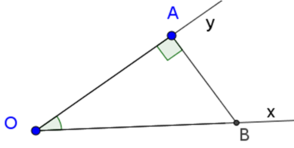
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
CM
4 tháng 5 2018
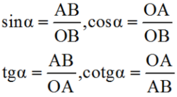
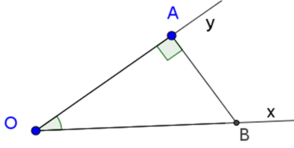
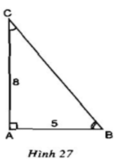
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
b) Áp dụng định lí pitago trong tam giác vuông OAB có:
O B 2 = O A 2 + A B 2
Từ đó ta có:
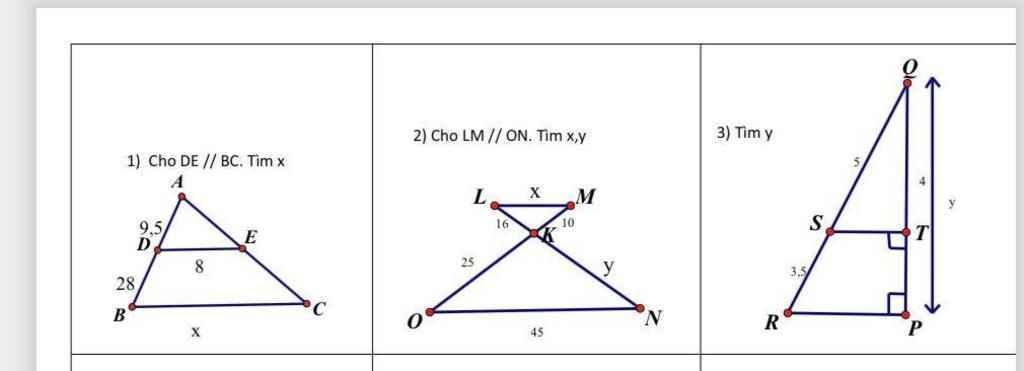
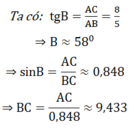
`1).`
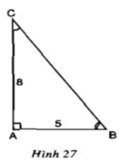
Ta có: `AB=AD+DB=9,5+28=37,5`
`\triangle ABC` có: `DE////BC`, theo hệ quả của định lí Ta-lét:
`(AD)/(AB)=(DE)/(BC)`
`=>(9,5)/(37,5)=8/x`
`=>x=(37,5.8)/(9,5)`
`=>x=600/19`
`2).`
`\triangle OKN` có: `LM////ON` theo hệ quả của định lí Ta-lét:
`(KO)/(KM)=(KN)/(KL)=(ON)/(LM)`
`=>25/10=y/16=45/x`
`=>y/16=45/x=5/2`
Với `y/16=5/2=>y=(16.5)/2=40`
Với `45/x=5/2=>x=(45.2)/5=18`
`3).`
Ta có: `ST \bot PQ` và `RP \bot PQ`
`=>ST //// RP`
Có: `QR=QS+SR=5+3,5=8,5`
`(QT)/(QP)=(QS)/(QR)`
`=>4/y=5/(8,5)`
`=>y=(4.8,5)/5`
`=>y=6,8`
`@Nae`