Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

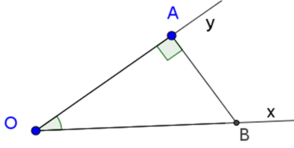
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:

b) Áp dụng định lí pitago trong tam giác vuông OAB có:
O B 2 = O A 2 + A B 2
Từ đó ta có:
![]()

Áp dụng định lí pitago trong tam giác vuông OAB có:
OB2 = OA2 + AB2
Từ đó ta có:
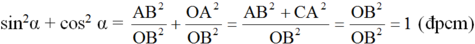

\(\frac{1-tana}{1+tana}=\frac{1-\frac{sina}{cosa}}{1+\frac{sina}{cosa}}=\frac{\frac{1}{cosa}\left(cosa-sina\right)}{\frac{1}{cosa}\left(cosa+sina\right)}=\frac{cosa-sina}{cosa+sina}\)

ta co \(sin^2a+cos^2a=1\Rightarrow cosa=0.36\)
\(\frac{sina}{cosa}=tana\Rightarrow tana=\frac{20}{9}\)
\(tana\cdot cotga=1\Rightarrow cotga=\frac{9}{20}\)
câu b tương tự nha cau c \(\frac{sina+cosa}{sina-cosa}=\) bn

Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay vào P ta được

\(\sin^2\alpha+\cos^2\alpha=1\\ \Rightarrow\cos^2\alpha=1-0,6^2=0,64\\ \Rightarrow\cos\alpha=0,8=\dfrac{4}{5}\\ \tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{0,6}{0,8}=\dfrac{3}{4}\\ \cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{1}{0,75}=\dfrac{4}{3}\)
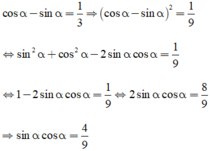
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có: