
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\sqrt{9.10}-3\sqrt{10-2.3.\sqrt{10}+9}\)
\(=3\sqrt{10}-3\sqrt{\left(\sqrt{10}-3\right)^2}\)
\(=3\sqrt{10}-3\left(\sqrt{10}-3\right)\)
\(=9\)

a) Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Lời giải:
$A=1+\frac{1}{\sqrt{x}-3}$
Để $A$ max thì $\sqrt{x}-3$ phải dương và nhỏ nhất.
Với $x$ nguyên, để $\sqrt{x}-3$ dương và nhỏ nhất thì $x=10$
Khi đó, $A_{\max}=1+\frac{1}{\sqrt{10}-3}=4+\sqrt{10}$
------------------
$B=1+\frac{1}{\sqrt{x}-2}$.
Lập luận tương tự phần a, ta thấy với $x$ nguyên không âm thì $\sqrt{x}-2$ đạt giá trị dương nhỏ nhất tại $x=5$
$\Rightarrow B_{\max}=1+\frac{1}{\sqrt{5}-2}=3+\sqrt{5}$

b: \(\Leftrightarrow x\sqrt{2}=2\sqrt{2}+5\sqrt{2}=7\sqrt{2}\)
hay x=7


\(A=\frac{2x-\sqrt{x}+8}{2\sqrt{x}-1}=\frac{\sqrt{x}\left(2\sqrt{x}-1\right)+8}{2\sqrt{x}-1}\)
\(=\frac{\sqrt{x}\left(2\sqrt{x}-1\right)}{2\sqrt{x}-1}+\frac{8}{2\sqrt{x}-1}=\sqrt{x}+\frac{8}{2\sqrt{x}-1}\)
Áp dụng BĐT Cô Si cho 2 số dương \(\sqrt{x}\)và \(\frac{8}{2\sqrt{x}-1}\)ta có :
\(\sqrt{x}+\frac{8}{2\sqrt{x}-1}\ge2\sqrt{\sqrt{x}.\frac{8}{2\sqrt{x}-1}}\)
\(\Rightarrow A_{min}\)\(\Leftrightarrow2\sqrt{\sqrt{x}.\frac{8}{2\sqrt{x}-1}}\)nhỏ nhất \(\Rightarrow x=0\)
Vậy \(A=0\)\(\Leftrightarrow\sqrt{x}=\frac{8}{2\sqrt{x}-1}\)( tự tính nha )
Phạm Thị Thùy Linh đây nhé
\(A=\frac{2x-\sqrt{x}+8}{2\sqrt{x}-1}=\frac{1}{2}\left(2\sqrt{x}-1+\frac{16}{2\sqrt{x}-1}\right)+\frac{1}{2}\ge\frac{9}{2}\)
Dấu "=" xảy ra khi \(x=\frac{25}{4}\)

a) Hàm số trên nghịch biến trên R vì:
\(1< \sqrt{5}\Rightarrow1-\sqrt{5}< 0\)
\(\Rightarrow\) hệ số \(a< 0\)
b) Khi \(x=1+\sqrt{5}\)
\(y=\left(1-\sqrt{5}\right)\left(1+\sqrt{5}\right)-1\)
\(y=1^2-\left(\sqrt{5}\right)^2-1\)
\(y=1-5-1\)
\(y=-5\)
c) Khi \(y=\sqrt{5}\) khi và chỉ khi:
\(\left(1-\sqrt{5}\right)x-1=\sqrt{5}\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)x=1+\sqrt{5}\)
\(\Leftrightarrow x=\dfrac{1+\sqrt{5}}{1-\sqrt{5}}\)
\(\Leftrightarrow x=\dfrac{\left(1+\sqrt{5}\right)^2}{1-5}\)
\(\Leftrightarrow x=-\dfrac{3+\sqrt{5}}{2}\)




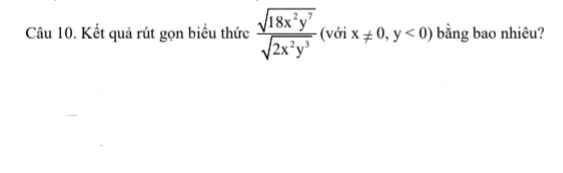

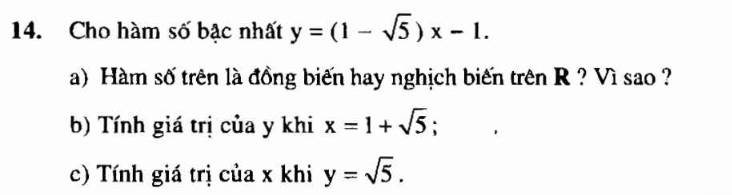 giúp e với aa, e cảm ơn nhiềuu
giúp e với aa, e cảm ơn nhiềuu
làm bài nào ?
đừng nói là làm hết nhé 'o'