
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


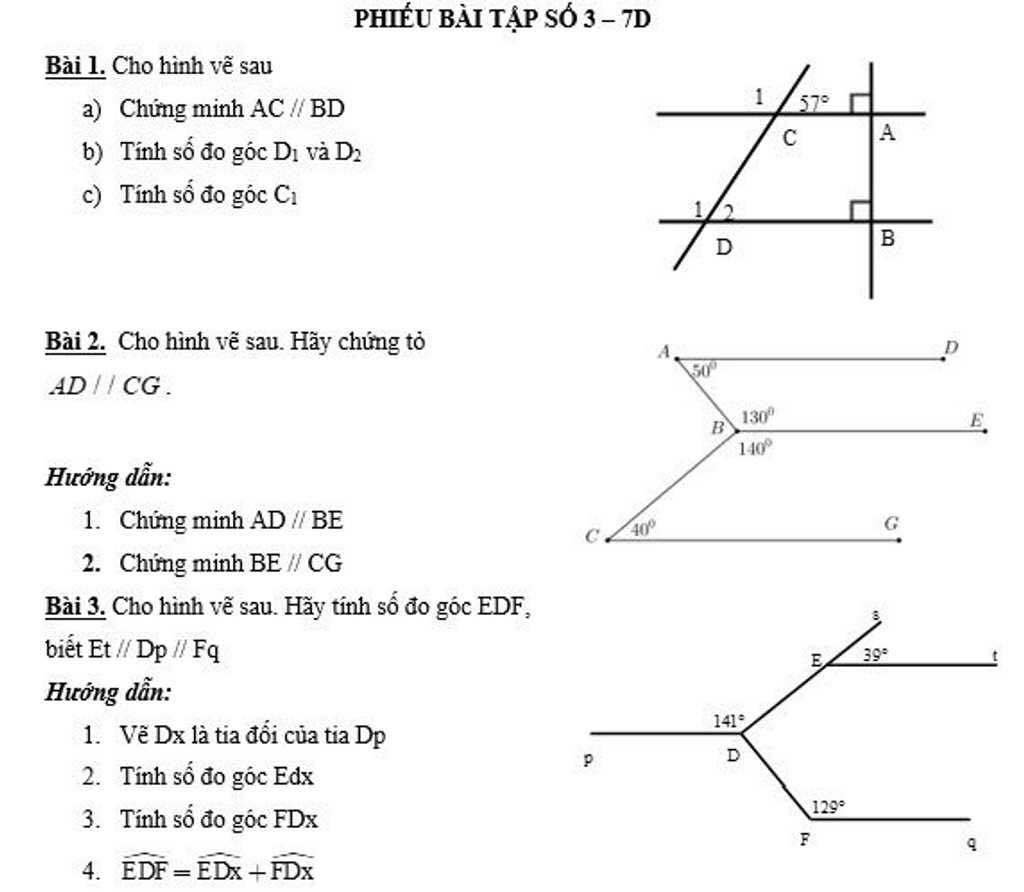
\(1,\\ a,\left\{{}\begin{matrix}AC\perp AB\\BD\perp AB\end{matrix}\right.\Rightarrow AC//BD\\ b,AC//BD\Rightarrow\widehat{D_2}=\widehat{C_1}=57^0\left(đồng.vị\right)\\ \widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_1}=180^0-57^0=123^0\\ c,AC//BD\Rightarrow\widehat{D_1}=\widehat{C_1}=123^0\left(đồng.vị\right)\)
\(2,\\ \widehat{DAB}+\widehat{ABE}=50^0+130^0=180^0\)
Mà 2 góc này ở vị trí TCP nên AD//BE (1)
\(\widehat{EBC}+\widehat{BCG}=140^0+40^0=180^0\)
Mà 2 góc này ở vị trí TCP nên BE//CG (2)
Từ (1)(2) ta được AD//CG

\(\widehat{XAB}\) + \(\widehat{ABZ}\) = 1300 + 500 = 1800
Vì góc XAB và góc ABZ là hai góc trong cùng phía nên
Ax // BZ
BZ // Cy ⇔ \(x\) + \(\widehat{yCB}\) =1800
⇒ \(x\) = 1800 - 1450 = 350

Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
Do đó: a=10; b=15;c=20

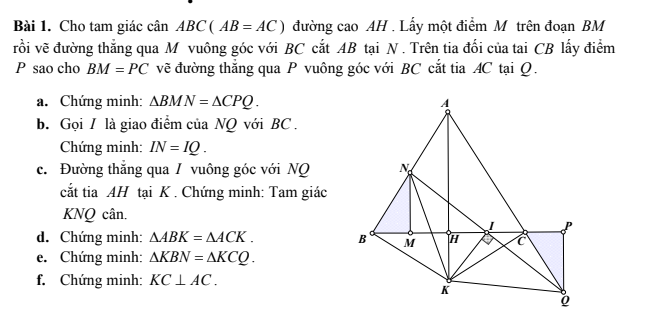
a, Vì tam giác ABC cân tại A nên \(\widehat{NBM}=\widehat{ACB}\)
Mà \(\widehat{ACB}=\widehat{PCQ}\left(đối.đỉnh\right)\Rightarrow\widehat{NBM}=\widehat{PCQ}\)
Mà \(\widehat{NMB}=\widehat{CPQ}=90^0;BM=PC\)
Do đó \(\Delta BMN=\Delta CPQ\left(g.c.g\right)\)
b, Vì \(BM//PQ\left(\perp BP\right)\) nên \(\widehat{MNI}=\widehat{IQP}\)
Mà \(\widehat{NMI}=\widehat{IPQ}=90^0;MN=PQ\left(\Delta BMN=\Delta CPQ\right)\)
Do đó \(\Delta IMN=\Delta IPQ\left(g.c.g\right)\)
\(\Rightarrow IN=IQ\)
c, Vì IK là đường cao cũng là trung tuyến tam giác KNQ nên tam giác KNQ cân tại K

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

a) Xét ΔNMD và ΔNED có
NM=NE(gt)
\(\widehat{MND}=\widehat{END}\)(ND là tia phân giác của \(\widehat{NME}\))
ND chung
Do đó: ΔNMD=ΔNED(c-g-c)
Suy ra: \(\widehat{NMD}=\widehat{NED}\)(hai góc tương ứng)
mà \(\widehat{NMD}=90^0\)(gt)
nên \(\widehat{NED}=90^0\)
hay DE\(\perp\)NP
b) Ta có: NM=NE(gt)
nên N nằm trên đường trung trực của ME(1)
Ta có: DM=DE(ΔNMD=ΔNED)
nên D nằm trên đường trung trực của ME(2)
Từ (1) và (2) suy ra ND là đường trung trực của ME

\(\left|x+\frac{5}{2}\right|+\left|\frac{2}{5}-x\right|=0\)
Có \(\left|x+\frac{5}{2}\right|\ge0\)với mọi x
\(\left|\frac{2}{5}-x\right|\ge0\)với mọi x
=> Để \(\left|x+\frac{5}{2}\right|+\left|\frac{2}{5}-x\right|=0\)=> \(\hept{\begin{cases}\left|x+\frac{5}{2}\right|=0\\\left|\frac{2}{5}-x\right|=0\end{cases}}\)
=> \(\hept{\begin{cases}x+\frac{5}{2}=0\\\frac{2}{5}-x=0\end{cases}}\)
=> \(\hept{\begin{cases}x=-\frac{5}{2}\\x=\frac{2}{5}\end{cases}}\)(Không thỏa mãn vì x không thể đồng thời nhận 2 giá trị)
=> Không có giá trị nào của x thỏa mãn đề bài
=> Số giá trị của x là 0
\(\left|x+\frac{5}{2}\right|\ge0\) và \(\left|\frac{2}{5}-x\right|\ge0\)
\(\Rightarrow\left|x+\frac{5}{2}\right|+\left|\frac{2}{5}-x\right|=0\Leftrightarrow\hept{\begin{cases}x+\frac{5}{2}=0\\\frac{2}{5}-x=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-\frac{5}{2}\\x=\frac{2}{5}\end{cases}}}\)
Vậy x có 2 giá trị.

 Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi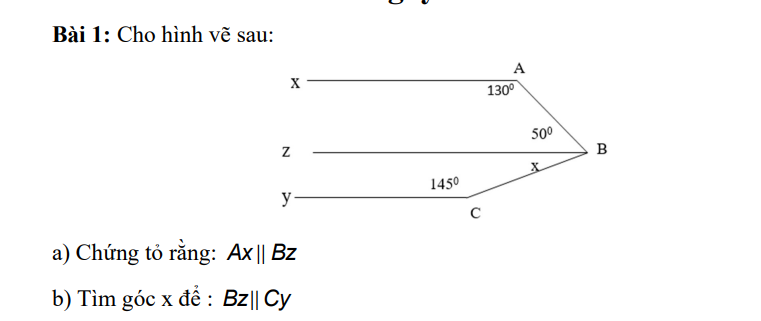 ai làm giúp mình với mình đang cần gấp lắm ạ
ai làm giúp mình với mình đang cần gấp lắm ạ



a, \(2y^2\left(8y^6\right)y=16y^9\)
b, \(=\dfrac{3}{4}x^3y^4\)
c, \(=10x^3y^4z^8\)
d, \(=\left(\dfrac{3}{4}x^2y^3\right)\left(\dfrac{12}{5}x^4\right)=\dfrac{9}{5}x^6y^3\)
e, \(=-\dfrac{5}{4}x^5y^{10}\)
f, \(=120x^4y^6z^4\)