K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 10 2021
bạn tự vẽ hình giúp mik nha
a. xét \(\Delta ADN\) và \(\Delta BAM\) có
AB=AD(gt)
\(\widehat{ADN}=\widehat{BAM}=90^o\)
DN=MA(N,M là trung điểm của cạnh DC,AD)
\(\Rightarrow\Delta ADN\sim\Delta BAM\left(c.g.c\right)\)
\(\Rightarrow\widehat{DNA}=\widehat{AMB}\)
mà:\(\widehat{DNA}+\widehat{DAN}=90^o\Rightarrow\widehat{BMA}+\widehat{DAN}=90^o\)
\(\Rightarrow\Delta MAI\) vuông tại I
\(\Rightarrow AI\perp MI\) hay \(MB\perp AN\)
b.ta có M là trung điểm của AD\(\Rightarrow AM=\dfrac{1}{2}AD=\sqrt{5}\)
trong \(\Delta MAB\) vuông tại A có
\(MB=\sqrt{AM^2+AB^2}=\sqrt{\sqrt{5^2}+\left(2\sqrt{5}\right)^2}=5\)
\(AM^2=MB.MI\Rightarrow MI=\dfrac{AM^2}{MB}=\dfrac{\sqrt{5^2}}{5^5}=0,2\)
\(AI.MB=AM.AB\Rightarrow AI=\dfrac{AM.AB}{MB}=\dfrac{\sqrt{5}.2\sqrt{5}}{5}\)=2
c.IB=MB-MI=5-0,2=4,8
\(S_{\Delta AIB}=\dfrac{AI.IB}{2}=\)\(\dfrac{2.4,8}{2}=4,8\)
\(S_{\Delta ADN}=\dfrac{AD.DN}{2}=\dfrac{2\sqrt{5}.\sqrt{5}}{2}=5\)
\(S_{\Delta ABCD}=\left(2\sqrt{5}\right)^2=20\)
\(S_{BINC}=S_{ABCD}-S_{\Delta AIB}-S_{\Delta DAN}\)=20-4,8-5=10,2
16 tháng 2 2022
a, \(\left\{{}\begin{matrix}35x-28y=21\\35x-45y=40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17y=-19\\x=\dfrac{3+4y}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{19}{17}\\x=-\dfrac{13}{17}\end{matrix}\right.\)
b, Đặt x;y khác 0
Đặt 1/x = t ; 1/y = u
\(\left\{{}\begin{matrix}t-8u=18\\5t+4u=51\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5t-40u=90\\5t+4u=51\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-44u=39\\t=18+8u\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u=-\dfrac{39}{44}\\t=\dfrac{120}{11}\end{matrix}\right.\)
Theo cách đặt y = -44/39 ; x = 11/120 (tm)
16 tháng 2 2022
\(a,\\ \Leftrightarrow\left\{{}\begin{matrix}35x-28y=21_{\left(1\right)}\\35x-45y=40_{\left(2\right)}\end{matrix}\right.\\ Lấy\left(1\right)-\left(2\right),ta.đc:\\ -17y=19\Leftrightarrow y=\dfrac{-19}{17}\\ Thay.vào.\left(1\right):\\ 35x-28.\dfrac{-19}{17}=21\Leftrightarrow x=\dfrac{-5}{17}\)
Vậy ......
\(b,\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=18+\dfrac{1}{y}\\5.\left(18+\dfrac{1}{y}\right)+\dfrac{4}{y}=51\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=18+\dfrac{1}{y}\\\dfrac{9}{y}=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=18-\dfrac{13}{3}\\\dfrac{1}{y}=\dfrac{-13}{3}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{41}{3}\\\dfrac{1}{y}=\dfrac{-13}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{41}\\y=\dfrac{-3}{13}\end{matrix}\right.\)
HK
3
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
31 tháng 8 2021
1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)
30 tháng 9 2021
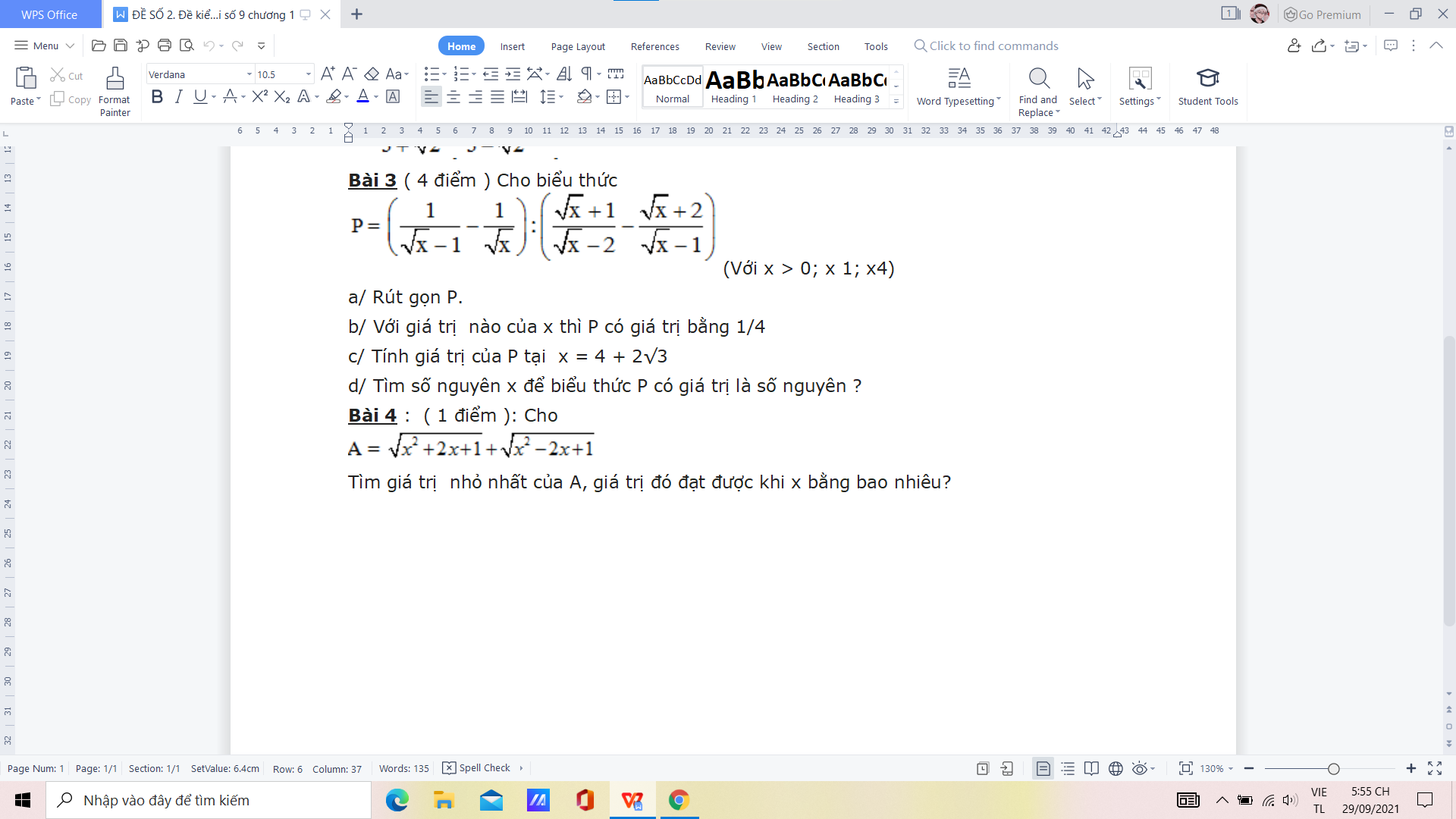
\(3,\\ a,P=\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\left(x>0;x\ne1;x\ne4\right)\\ P=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{x-1-x+4}\\ P=\dfrac{\sqrt{x}-2}{3\sqrt{x}}\\ b,P=\dfrac{1}{4}\Leftrightarrow\dfrac{\sqrt{x}-2}{3\sqrt{x}}=\dfrac{1}{4}\Leftrightarrow4\sqrt{x}-8=3\sqrt{x}\\ \Leftrightarrow\sqrt{x}=8\Leftrightarrow x=64\)
\(c,x=4+2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\\ \Leftrightarrow P=\dfrac{\sqrt{3}+1-2}{3\left(\sqrt{3}+1\right)}=\dfrac{\sqrt{3}-1}{3\sqrt{3}+3}=\dfrac{\left(\sqrt{3}-1\right)\left(3\sqrt{3}-3\right)}{18}\\ P=\dfrac{12-6\sqrt{3}}{18}=\dfrac{2-\sqrt{3}}{3}\)
\(d,P\in Z\Leftrightarrow3P\in Z\Leftrightarrow\dfrac{3\sqrt{x}-6}{3\sqrt{x}}\in Z\Leftrightarrow1-\dfrac{6}{3\sqrt{x}}\in Z\\ \Leftrightarrow6⋮3\sqrt{x}\Leftrightarrow3\sqrt{x}\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{1;2;3;6\right\}\left(\sqrt{x}\ge0\right)\\ \Leftrightarrow x\in\left\{1;4;9;36\right\}\)
30 tháng 9 2021
\(4,\\ A=\sqrt{x^2+2x+1}+\sqrt{x^2-2x+1}\\ A=\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-1\right)^2}\\ A=\left|x+1\right|+\left|x-1\right|\\ A=\left|x+1\right|+\left|1-x\right|\ge\left|x+1+1-x\right|=\left|2\right|=2\)
Dấu \("="\Leftrightarrow x=1\)
10 tháng 10 2021
Bài 11:
a: \(\sqrt{18}+3\sqrt{50}-\sqrt{98}\)
\(=3\sqrt{2}+15\sqrt{2}-7\sqrt{2}\)
\(=11\sqrt{2}\)
c: \(\sqrt{20}+\sqrt{80}-\sqrt{45}\)
\(=2\sqrt{5}+4\sqrt{5}-3\sqrt{5}\)
\(=3\sqrt{5}\)
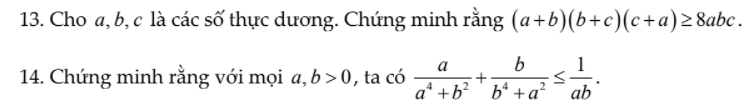
Bài 1:
a) Ta có: \(A=\left(\dfrac{6+\sqrt{20}}{3+\sqrt{5}}+\dfrac{\sqrt{14}-\sqrt{2}}{\sqrt{7}-1}\right):\left(2+\sqrt{2}\right)\)
\(=\left(2+\sqrt{2}\right)\cdot\dfrac{1}{2+\sqrt{2}}\)
=1
b) Ta có: \(B=\sqrt{5-2\sqrt{6}}+\sqrt{5+2\sqrt{6}}-\dfrac{11}{2\sqrt{3}+1}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}-2\sqrt{3}+1\)
=1
Bài 2:
b) Ta có: \(\sqrt{9x^2-9}+\sqrt{4x^2-4}=\sqrt{16x^2-16}+2\)
\(\Leftrightarrow3\sqrt{x^2-1}+2\sqrt{x^2-1}-4\sqrt{x^2-1}=2\)
\(\Leftrightarrow x^2-1=4\)
\(\Leftrightarrow x\in\left\{\sqrt{5};-\sqrt{5}\right\}\)