Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


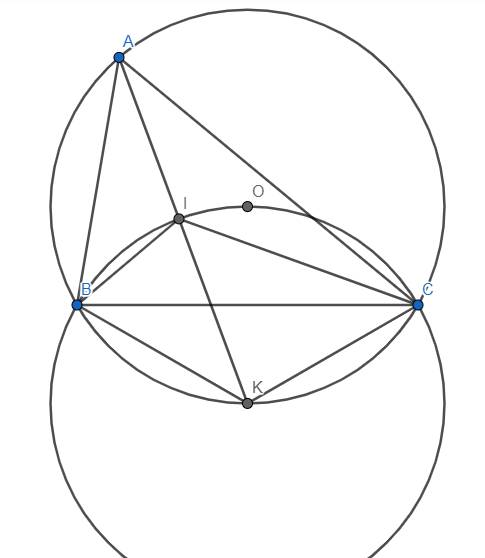
Gọi (O) là đường tròn ngoại tiếp tam giác ABC, AI cắt (O) tại K. Theo bổ đề quen thuộc thì K là tâm của (BIC). Hơn nữa \(\widehat{BIC}=90^o+\dfrac{\widehat{BAC}}{2}=120^o\) và \(\widehat{BOC}=2\widehat{BAC}=120^o\) nên \(\widehat{BIC}=\widehat{BOC}\), suy ra tứ giác BIOC nội tiếp, suy ra \(O\in\left(K\right)\). Điều này có nghĩa bán kính của \(\left(K\right)\) chính là \(OK=2\).


5:
(d) vuông góc 2x-y-2018=0
=>(d): x+2y+c=0
(C): x^2+4x+4+y^2-6y+9-25=0
=>(x+2)^2+(y-3)^2=25
=>R=5; I(-2;3)
Theo đề, ta có: d(I;(d))=5
=>\(\dfrac{\left|1\cdot\left(-2\right)+2\cdot3+c\right|}{\sqrt{5}}=5\)
=>|c+4|=5căn 5
=>c=5căn5-4 hoặc c=-5căn 5-4

\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=a\sqrt{5}\)
\(\left|\overrightarrow{BC}-\overrightarrow{OD}\right|=\left|\overrightarrow{AD}+\overrightarrow{DO}\right|=AO=\dfrac{a\sqrt{5}}{2}\)

1: \(\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)

\(sin\left(\dfrac{\pi}{2}-x\right)+1=cosx+1=\dfrac{4}{5}+1=\dfrac{9}{5}\)

\(\overrightarrow{AB}=\left(2-1;6-5\right)=\left(1;1\right)\)

`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)