Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Ta có:
\(2xy=(x+y)^2-(x^2+y^2)=2^2-8=-4\Rightarrow xy=-2\)
Vậy:
\(M=x^3+x^4+y^3+y^4=(x^3+y^3)+(x^4+y^4)\)
\(=(x+y)(x^2+y^2)-xy(x+y)+(x^2+y^2)^2-2x^2y^2\)
\(=2.8-(-2).2+8^2-2(-2)^2\)
\(=76\)
b)
\(M=x^2+y^2+2xy-4x-4y+3\)
\(=(x^2+xy)+(y^2+xy)-4(x+y)+3\)
\(=x(x+y)+y(x+y)-4(x+y)+3\)
\(=(x+y)(x+y)-4(x+y)+3\)
\(=5.5-4.5+3=8\)

a, Thay x = -2 ; y = 3 ta được
\(A=\dfrac{4\left(-2\right)-5.3}{8\left(-2\right)-7.3}=\dfrac{-8-15}{-16-21}=\dfrac{23}{37}\)
b, Ta có \(\dfrac{x}{y}=\dfrac{5}{4}\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=k\Rightarrow x=5k;y=4k\)
Thay vào ta được \(A=\dfrac{4.5k-5.4k}{8.5k-7.4k}=\dfrac{0}{40k-28k}=0\)

a)Theo tính chất đại lượng tỉ lệ thuận ta có:
\(\frac{y1}{x1}=\frac{y2}{x2}\)\(\Rightarrow\)\(\frac{-3}{x1}\)=\(\frac{-2}{5}\)\(\Rightarrow\)x1=\(\frac{-3.5}{-2}\)=\(\frac{15}{2}\)
b)tương tự ta giải được x2=\(\frac{20}{3}\)
làm câu b cho mk luôn thử xem
câu a mk làm gióng bạn ồi

a: k=-2/5
=>y=-2/5x
Khi x=-1 thì y=2/5
b: Khi y=3 thì -2/5x=3
hay x=3:(-2/5)=-3x5/2=-15/2

ối lắm thế :((
3.
a/ Giả sử đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ là k
=> y = k/x
Thay x = 8 ; y = 15 vào ct y = k/x ta có
\(\dfrac{k}{8}=15\Rightarrow k=120\)
Thay \(k=120\) vào ct \(y=\dfrac{k}{x}\) ta có
\(y=\dfrac{120}{x}\)
b/ Thay x = 6 vào ct \(y=\dfrac{120}{x}\) ta có
\(y=\dfrac{120}{6}=20\)
Thay x = - 10 vào ct \(y=\dfrac{120}{x}\) ta có
\(y=\dfrac{120}{-10}=-12\)
b/ Thay y = 2 vào ct \(y=\dfrac{120}{x}\) ta có
\(2=\dfrac{120}{x}\Rightarrow x=60\)
Thay y = - 30 vào ct \(y=\dfrac{120}{x}\) ta có
\(-30=\dfrac{120}{x}\Rightarrow x=-4\)
4/
a/ Giả sử đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ là k
=> y = xk
Thay y = 4 ; x = 6 vào ct y = xk ta có
\(4=6k\Rightarrow k=\dfrac{2}{3}\)
Thay \(k=\dfrac{2}{3}\) vào ct y = xk ta có
\(y=\dfrac{2}{3}x\)
b/ Thay x = 9 vào ct \(y=\dfrac{2}{3}x\) ta có
\(y=\dfrac{2}{3}.9=6\)
Thay y = - 8 vào ct \(y=\dfrac{2}{3}x\) ta có
\(-8=\dfrac{2}{3}x\Rightarrow x=-12\)
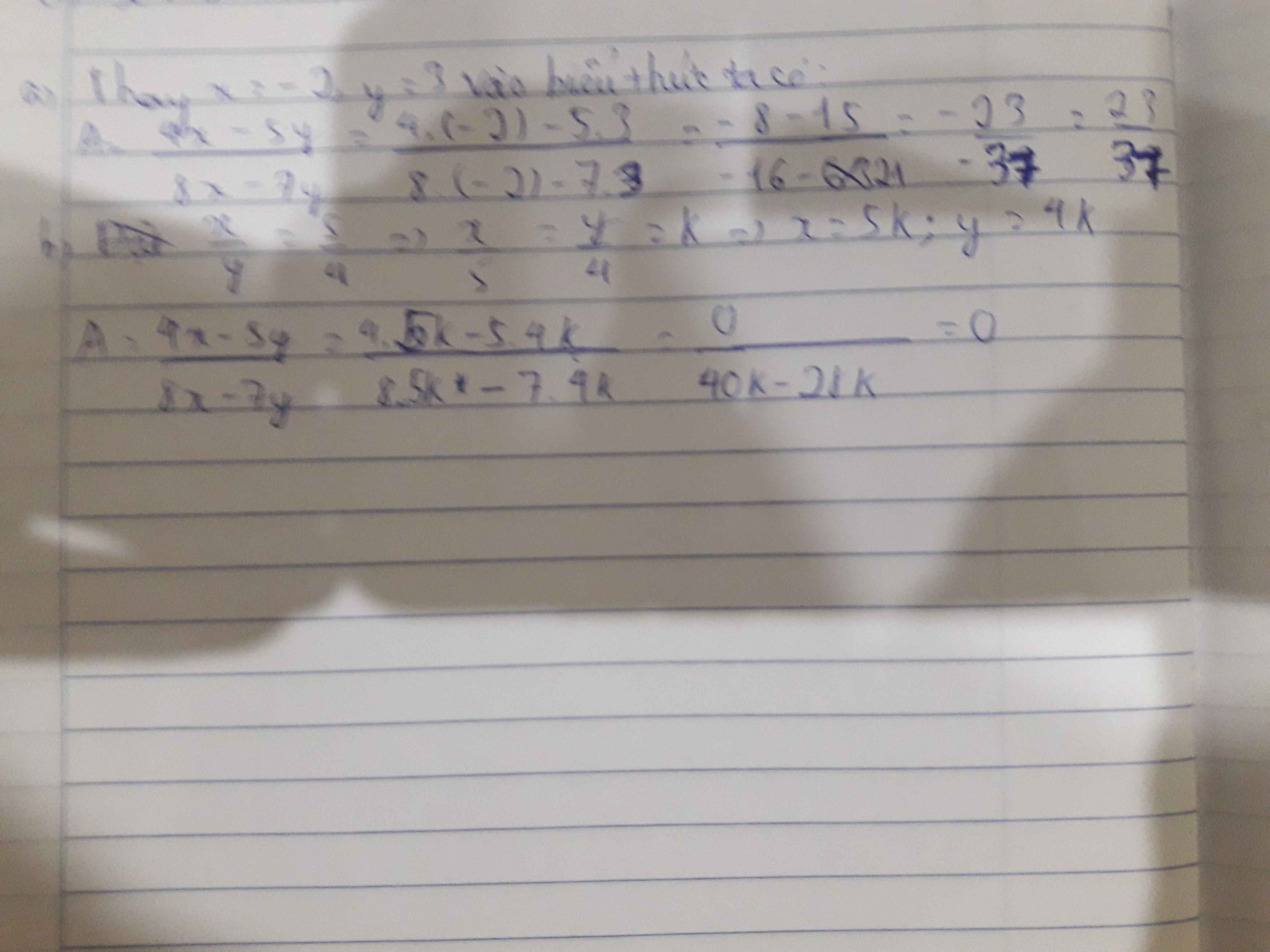
a, \(x^2+y^2=8\Rightarrow\left(x+y\right)^2-2xy=8\Rightarrow xy=\frac{8-\left(x+y\right)^2}{-2}=\frac{8-4}{-2}=-2\)
=>\(M=x^3+x^4+y^3+y^4=\left(x+y\right)^3-3xy\left(x+y\right)+\left(x^2+y^2\right)^2-2x^2y^2\)
\(=2^3-3.\left(-2\right).2+8^2-2.\left(-2\right)^2=76\)
b, \(M=x^2+y^2+2xy-4x-4y+3=\left(x+y\right)^2-4\left(x+y\right)+4-1=\left(x+y-2\right)^2-1=\left(5-2\right)^2-1=8\)