
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc AMB=1/2*180=90 độ
góc AMN+góc AKN=180 độ
=>AMNK là tứ giác nội tiếp
b: ΔCAB vuông tại A có AM vuông góc CB
nên CA^2=MC*CB


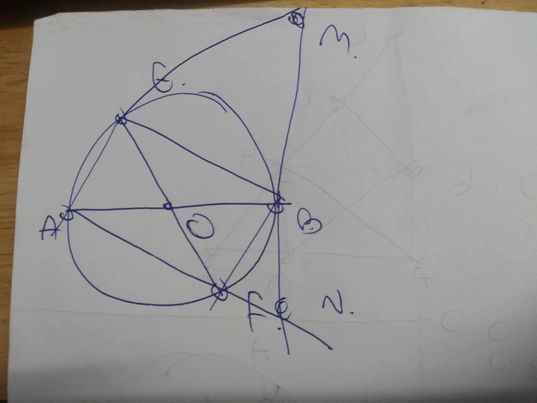
a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
b: Xét (O) có
ΔCND nội tiếp
CD là đường kính
Do đó: ΔCND vuông tại N
=>CN\(\perp\)ND tại N
=>CN\(\perp\)AD tại N
Xét ΔDCA vuông tại C có CN là đường cao
nên \(AN\cdot AD=AC^2\left(3\right)\)
Ta có: OA là trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOCA vuông tại C có CH là đường cao
nên \(AH\cdot AO=AC^2\left(4\right)\)
Từ (3) và (4) suy ra \(AN\cdot AD=AH\cdot AO\)
c: Ta có: \(AH\cdot AO=AN\cdot AD\)
=>\(\dfrac{AH}{AD}=\dfrac{AN}{AO}\)
Xét ΔAHN và ΔADO có
\(\dfrac{AH}{AD}=\dfrac{AN}{AO}\)
\(\widehat{HAN}\) chung
Do đó: ΔAHN đồng dạng với ΔADO
=>\(\widehat{AHN}=\widehat{ADO}\)
Ta có: ΔOCA vuông tại C
=>\(CO^2+CA^2=OA^2\)
=>\(CA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(CA=R\sqrt{3}\)
Ta có: ΔDCA vuông tại C
=>\(DC^2+CA^2=DA^2\)
=>\(DA^2=\left(2R\right)^2+\left(R\sqrt{3}\right)^2=7R^2\)
=>\(DA=R\sqrt{7}\)
Xét ΔDCA vuông tại C có \(sinCDA=\dfrac{CA}{DA}\)
=>\(sinCDA=\dfrac{R\sqrt{3}}{R\sqrt{7}}=\sqrt{\dfrac{3}{7}}=\dfrac{\sqrt{21}}{7}\)
=>\(sinAHN=\dfrac{\sqrt{21}}{7}\)

b) Gọi (d3): y=ax+b
Vì (d3)//(d1) nên \(a=-\dfrac{2}{3}\)
Vậy: (d3): \(y=\dfrac{-2}{3}x+b\)
Thay x=6 vào (d2), ta được:
\(y=-2\cdot6+4=-12+4=-8\)
Thay x=6 và y=-8 vào (d3), ta được:
\(\dfrac{-2}{3}\cdot6+b=-8\)
\(\Leftrightarrow b=-4\)
Vậy: (d3): \(y=\dfrac{-2}{3}x-4\)


Ta cóBDA+ADC=BDC 10\(^o\)+50\(^o\)=60\(^o\)
Xét tam giác ADCvuông tại C:
\(AC=CD.tanADC\)
\(\Rightarrow AC=40.tan50^o\)
\(\Leftrightarrow AC\approx47,67cm\)
Xét tam giác BDC vuông tại C có:
\(CB=CD.\tan BDC\)
\(\Rightarrow CB=40.tan60^o\)
\(\Leftrightarrow CB\approx69,28cm\)
Ta có \(AB=BC-AC=69,28-47,67=21,61cm\)
 A,B vs vẽ hình thôi ạ
A,B vs vẽ hình thôi ạ vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á
vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á vẽ hình hộ thôi ạ
vẽ hình hộ thôi ạ




CHÚC EM HỌC TỐT NHA