Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

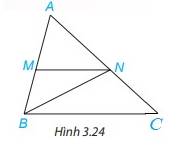
a) Góc MNB so le trong với góc NBC
b) Góc ACB đồng vị với góc ANM
c) Các cặp góc trong cùng phía là: góc MNC và góc NCB; góc NMB và góc MBC
d) Vì MN//BC nên
\(\widehat {ANM} = \widehat {ACB}\) (2 góc đồng vị)
\(\widehat {AMN} = \widehat {ABC}\) (2 góc đồng vị)
\(\widehat {MNB} = \widehat {NBC}\) ( 2 góc so le trong)

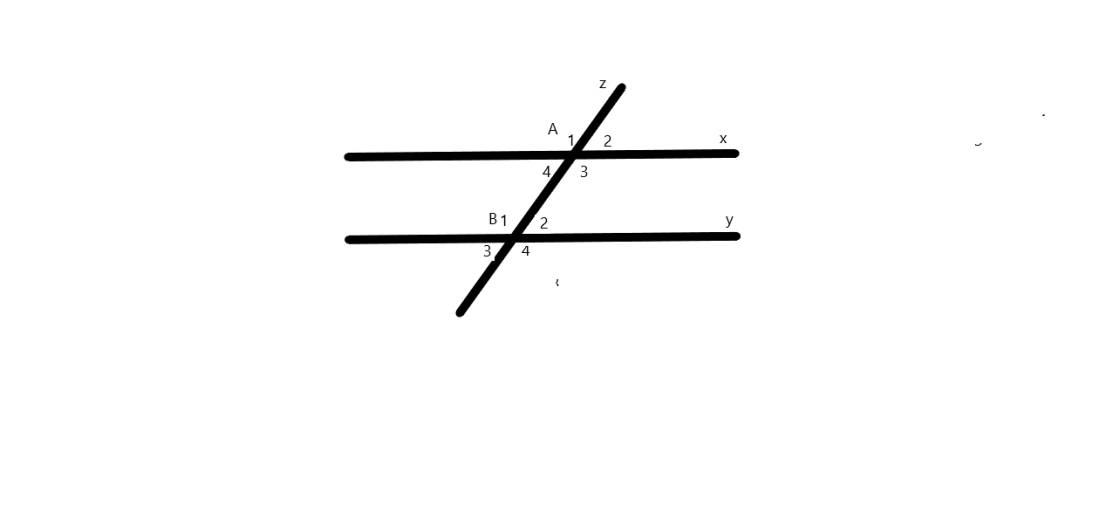
a: So le trong: góc A4 và góc B2, góc A3 và góc B1
Đồng vị: góc A1 và góc B1; góc B2 và góc A2; góc A3 và góc B3; góc A4 và góc B4
Trong cùng phía: góc A4 và góc B1; góc A3 và góc B2
b: góc A4=góc A2=60 độ
góc A1=góc A3=180-60=120 độ
góc B3=góc B2=60 độ
góc B1=góc B4=180-60=120 độ
c: góc A2=góc B2
mà hai góc này đồng vị
nên Ax//By

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

a) cặp góc đới đỉnh là: AOD và BOC , AOB và DOC
b) góc kề bù với aob: AOD,BOC
c)cặp góc slt: ABD và BDC, BAC và ACD
d)cặp góc tcp: BAD và CDA,ABC và DCB,ADC và BCD,DAB và CBA;AOD và DAO,ADO và AOD,ODA và OAD;...(xét tiếp các tam giác khác ra các góp trong cùng phía)

Bạn vẽ hình ra đi mình giúp
Mình ko thích vẽ hình lắm
Chúc bạn học tốt
@@
bạn giúp mk luôn đi,mk kobiết gửi trên mt thé nào .xong mk cho
 a) k
a) k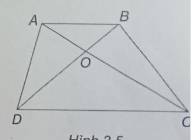
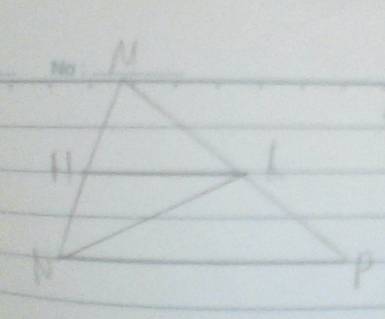
a) Để tìm một góc so le với góc HKM, chúng ta có thể chọn góc KHN. b) Để tìm một góc đồng vị với góc MKH, chúng ta có thể chọn góc HKM. c) Có hai cặp góc trong cùng phía, đó là cặp góc HKM và góc KHN, cũng như cặp góc MKH và góc KHN. d) Với điều kiện HK song song với MN, ta có thể kể tên ba cặp góc bằng nhau là góc HKM và góc MHN, góc KHN và góc MNH, cũng như góc MKH và góc NHM