Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(x^4-4x^3-6x^2-4x+1=0\)(*)
<=> \(x^4+4x^2+1-4x^3-4x+2x^2-12x^2=0\)
<=> \(\left(x^2-2x+1\right)^2=12x^2\)
<=>\(\left(x-1\right)^4=12x^2\) <=> \(\left[{}\begin{matrix}\left(x-1\right)^2=\sqrt{12}x\\\left(x-1\right)^2=-\sqrt{12}x\end{matrix}\right.\)<=> \(\left[{}\begin{matrix}x^2-2x+1-\sqrt{12}x=0\left(1\right)\\x^2-2x+1+\sqrt{12}x=0\left(2\right)\end{matrix}\right.\)
Giải (1) có: \(x^2-2x+1-\sqrt{12}x=0\)
<=> \(x^2-2x\left(1+\sqrt{3}\right)+\left(1+\sqrt{3}\right)^2-\left(1+\sqrt{3}\right)^2+1=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2-3-2\sqrt{3}=0\)
<=> \(\left(x-1-\sqrt{3}\right)^2=3+2\sqrt{3}\) <=> \(\left[{}\begin{matrix}x-1-\sqrt{3}=\sqrt{3+2\sqrt{3}}\\x-1-\sqrt{3}=-\sqrt{3+2\sqrt{3}}\end{matrix}\right.\) <=> \(\left[{}\begin{matrix}x=\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(ktm\right)\\x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\left(tm\right)\end{matrix}\right.\)
=> \(x=-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)
Giải (2) có: \(x^2-2x+1+\sqrt{12}x=0\)
<=> \(x^2-2x\left(1-\sqrt{3}\right)+\left(1-\sqrt{3}\right)^2-\left(1-\sqrt{3}\right)^2+1=0\)
<=> \(\left(x+\sqrt{3}-1\right)^2=3-2\sqrt{3}\) .Có VP<0 => PT (2) vô nghiệm
Vậy pt (*) có nghiệm x=\(-\sqrt{3+2\sqrt{3}}+\sqrt{3}+1\)

Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm 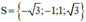
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
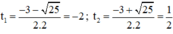
t 1 = - 2 < 0 nên loại.
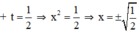
Vậy phương trình có tập nghiệm 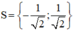
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
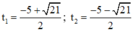
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.

a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
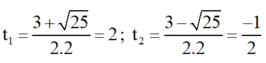
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
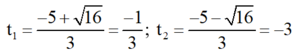
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.

2x4 + 3x2 – 2 = 0 (1)
Đặt x2 = t, t ≥ 0.
(1) trở thành: 2t2 + 3t – 2 = 0 (2)
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 32 – 4.2.(-2) = 25 > 0
⇒ (2) có hai nghiệm
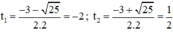
t1 = -2 < 0 nên loại.
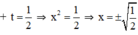
Vậy phương trình có tập nghiệm 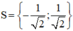

2x4 – 3x2 – 2 = 0; (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 2t2 – 3t – 2 = 0 (2)
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = (-3)2 - 4.2.(-2) = 25 > 0
⇒ Phương trình có hai nghiệm
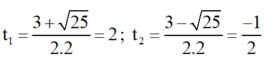
Chỉ có giá trị t1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.

a: \(2x^4-3x^2-5=0\)
\(\Leftrightarrow2x^4-5x^2+2x^2-5=0\)
\(\Leftrightarrow2x^2-5=0\)
\(\Leftrightarrow x^2=\dfrac{5}{2}\)
hay \(x\in\left\{\dfrac{\sqrt{10}}{2};-\dfrac{\sqrt{10}}{2}\right\}\)
b: Thay x=-2 và y=12 vào (P), ta được:
4(m2-1)=12
=>m2-1=3
=>m=2 hoặc m=-2

Bài 1:
$2x^4-3x^2-5=0$
$\Leftrightarrow (2x^4+2x^2)-(5x^2+5)=0$
$\Leftrightarrow 2x^2(x^2+1)-5(x^2+1)=0$
$\Leftrightarrow (x^2+1)(2x^2-5)=0$
$\Leftrightarrow 2x^2-5=0$ (do $x^2+1\geq 1>0$ với mọi $x\in\mathbb{R}$)
$\Leftrightarrow x^2=\frac{5}{2}$
$\Leftrightarrow x=\pm \sqrt{\frac{5}{2}}$
Bài 2:
a. Khi $m=1$ thì pt trở thành:
$x^2-6x+5=0$
$\Leftrightarrow (x^2-x)-(5x-5)=0$
$\Leftrightarrow x(x-1)-5(x-1)=0$
$\Leftrightarrow (x-1)(x-5)=0$
$\Leftrightarrow x-1=0$ hoặc $x-5=0$
$\Leftrightarrow x=1$ hoặc $x=5$
b.
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta=(m+5)^2-4(-m+6)\geq 0$
$\Leftrightarrow m^2+14m+1\geq 0(*)$
Áp dụng định lý Viet:
$x_1+x_2=m+5$
$x_1x_2=-m+6$
Khi đó:
$x_1^2x_2+x_1x_2^2=18$
$\Leftrightarrow x_1x_2(x_1+x_2)=18$
$\Leftrightarrow (m+5)(-m+6)=18$
$\Leftrightarrow -m^2+m+12=0$
$\Leftrightarrow m^2-m-12=0$
$\Leftrightarrow (m+3)(m-4)=0$
$\Leftrightarrow m=-3$ hoặc $m=4$
Thử lại vào $(*)$ thấy $m=4$ thỏa mãn.

\(A=\dfrac{3x^2+12x+17}{x^2+4x+5}=\dfrac{3\left(x^2+4x+5\right)+2}{x^2+4x+5}=3+\dfrac{2}{x^2+4x+5}\)
Ta có: \(x^2+4x+5=x^2+4x+4+1=\left(x+2\right)^2+1\ge1\)
\(\Rightarrow\dfrac{2}{x^2+4x+5}\le2\Rightarrow A\le3+2=5\)
\(\Rightarrow A_{max}=5\) khi \(x=-2\)