
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
x-y+5k=0 => y = x + 5k (1)
(2k - 3)x + k(y - 1) = 0 (2)
(k + 1)x - y + 1 = 0 => y = (k + 1)x + 1 (3)
Phương trình hoành độ giao điểm của (1) và (3) :
x + 5k = (k + 1)x + 1
<=> kx + 1 = 5k <=> x = (5k - 1)/k (k # 0)
Khi đó y = (5k - 1)/k + 5k = (5k^2 + 5k - 1)/k
Thay x = (5k - 1)/k và y = (5k^2 + 5k - 1)/k vào (2) :
(2k - 3).(5k - 1)/k + k.[(5k^2 + 5k - 1)/k - 1] = 0
<=> (2k - 3)(5k - 1)/k + k.(5k^2 + 4k - 1)/k = 0
<=> 10k^2 - 17k + 3 + 5k^3 + 4k^2 - k = 0
<=> 5k^3 + 14k^2 - 17k + 3 = 0
=> k = 0,2

1.
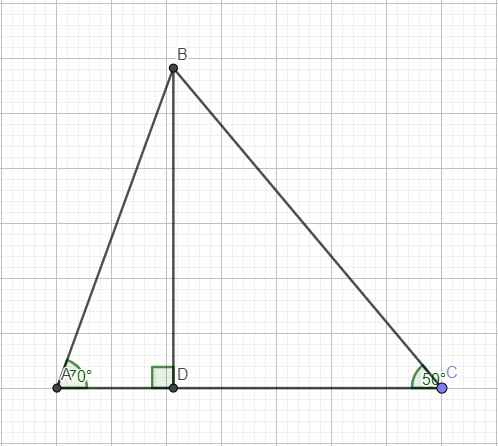
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
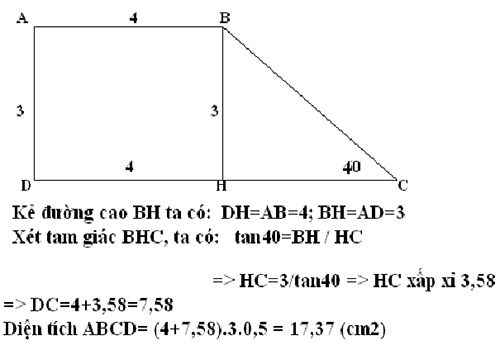
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)




1
e) E >= 2021
dấu = xảy ra khi x=1/2
g) G = |x-1|+ |2-x| >= |x-1+2-x|=1
Dấu = xảy ra khi (x-1)(2-x)>=0 <=> 1<=x<=2
h) H = |x-1|+|x-2| + |x-3|
Ta có : |x-1| + |x-3| = |x-1| + |3-x| >= |x-1+3-x| = 2
|x-2| >=0
=> H>=2
Dấu = xảy ra khi (x-1)(3-x) >=0 ; x-2=0
<=> x=2
k) K = |x-1| + |2x-1|
2K = |2x-2| + |2x-1| + |2x-1|
Ta có : |2x-2| + |2x-1| = |2x-2| + |1-2x| >= |2x-2+1-2x|=1
|2x-1| >=0
Dấu = xảy ra (2x-2)(1-2x) >=0; 2x-1=0
<=> x=1/2
e)Vì \(\left|x-\dfrac{1}{2}\right|\ge0\forall x\)
\(\Leftrightarrow2\left|x-\dfrac{1}{2}\right|\ge0\forall x\\ \Rightarrow2\left|x-\dfrac{1}{2}\right|+2012\ge2012\forall x\)
Dấu "=" xảy ra khi x=\(\dfrac{1}{2}\)
Vậy...
b)G=|x-1|+ |2-x|\(\)
áp dụng bđt |a+b|+ |c+d|\(\ge\left|a+b+c+d\right|\forall x\)
\(\Rightarrow\)ta có |x-1|+ |2-x|\(\ge\) \(\left|x-1+2-x\right|\forall x\)
\(\Leftrightarrow\text{|x-1|+ |2-x| }\ge1\forall x\)
Dấu "=" xảy ra khi 1\(\le x\le2\) \(\forall x\)
Vậy...
h)H= |x-1|+|x-2| + |x-3|
Ta có |x-1| + |x-3|
=|x-1| + |3-x| ( trong giá trị tuyệt đối đổi dấu không cần đặt dấu trừ ở ngoài)
=>|x-1| + |3-x|\(\ge\left|x-1+3-x\right|\forall x\)
<=>|x-1| + |3-x|\(\ge2\forall x\) (1)
Mà |x-2|\(\ge0\forall x\) (2)
Từ (1) và (2)=> ta có |x-1|+|x-2| + |x-3| \(\ge2\forall x\)
Dấu "=" xảy ra khi x-2=0
<=>x=2
Vậy...
k) K = |x-1| + |2x-1|
2K = |2x-2| + |2x-1| + |2x-1|
Mà : |2x-2| + |2x-1|
=|2x-2| + |1-2x|\(\ge\text{|2x-2+1-2x|}\) \(\forall x\)
Lại có |2x-1| \(\ge\)0 \(\forall x\)
Dấu "=" xảy ra 2x-1=0
<=>x=\(\dfrac{1}{2}\)
Vậy....
900+100=1000
700+x=1000
x= 1000-700
x= 300
ai k mình mình k lại
900 + 100
= 1000
700 + x = 1000
x = 1000 - 700
x = 300