
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


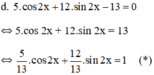
Vì 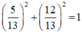 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn
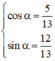
(*) ⇔ cos α.cos 2x + sin α. sin 2x = 1
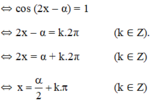
Vậy phương trình có họ nghiệm
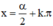 (k ∈ Z)
(k ∈ Z)
với α thỏa mãn 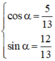

\(f'\left(x\right)=x^2+2x\)
a.
\(f'\left(-3\right)=3\) ; \(f\left(-3\right)=-2\)
Phương trình tiếp tuyến:
\(y=3\left(x+3\right)-2\Leftrightarrow y=3x+7\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm, do hệ số góc tiếp tuyến bằng 3
\(\Rightarrow f'\left(x_0\right)=3\Rightarrow x_0^2+2x_0=3\Rightarrow x_0^2+2x_0-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=1\Rightarrow y_0=-\dfrac{2}{3}\\x_0=-3\Rightarrow y_0=-2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=3\left(x-1\right)-\dfrac{2}{3}=3x-\dfrac{11}{3}\\y=3\left(x+3\right)-2=3x+7\end{matrix}\right.\)
c. Tiếp tuyến song song (d) nên có hệ số góc bằng 8
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow x_0^2+2x_0=8\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{14}{3}\\x_0=-4\Rightarrow y_0=-\dfrac{22}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=8\left(x-2\right)+\dfrac{14}{3}=...\\y=8\left(x+4\right)-\dfrac{22}{3}=...\end{matrix}\right.\)

a) `f^((n)) (x) = ((x+10)^6)^((n)) = 0 (n>6)`
b) `f^((n)) (x) = (cosx)^((n)) = cos(x+ (nπ)/2)`
c) `f^((n)) (x) = (sinx)^((n)) = sin(x + (nπ)/2)`

\(4\sin^22x-4\cos2x-1=0\)
\(\Leftrightarrow4\left(1-\cos^22x\right)-4\cos2x-1=0\)
\(\Leftrightarrow4-4\cos^22x-4\cos2x-1=0\)
\(\Leftrightarrow-4\cos^22x-4\cos2x+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\cos2x=\dfrac{-3}{2}\left(L\right)\end{matrix}\right.\Leftrightarrow\cos2x=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}-k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}-k\pi\end{matrix}\right.\left(k\in Z\right)\)
Chọn A

a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2 ⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3 ⇔ cos(x +π/3) = √2/2 ⇔ b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1. Đặt α = arccos thì phương trình trở thành cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π ⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5). c) Ta có sinx + cosx = √2cos(x – π/4) nên phương trình tương đương với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2 ⇔ d) 5cos2x + 12sin2x -13 = 0 ⇔ Đặt α = arccos5/13 thì phương trình trở thành cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1 ⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).

Hướng dẫn giải
Chọn B.
Ta có: 4sin4 + 12cos2 x – 7 =0
ó 4sin4x – 12sin2 x + 5= 0
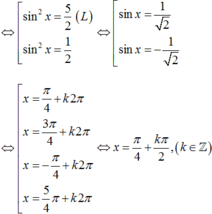

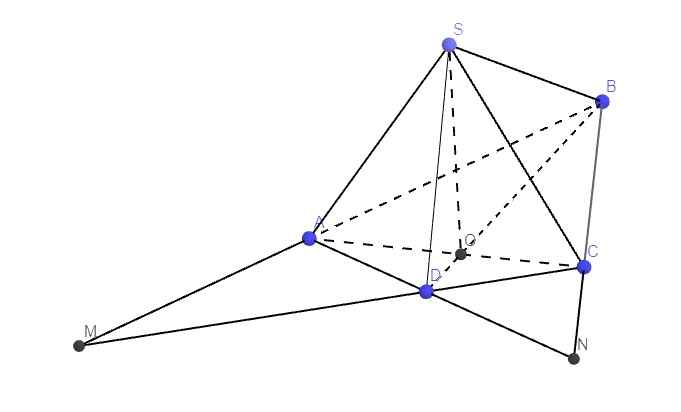
\(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow S=\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)

 giúp mình với mn ơi
giúp mình với mn ơi
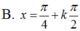

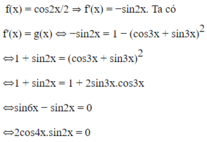
Chắc bạn ghi nhầm đề, 2 cái kia 1 cái là sin2x mới đúng