TQ
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 11
Đây là toán nâng cao chuyên đề tìm phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp đánh giá như sau:
Giải:
20\(^x\) : 14\(^x\) = \(\dfrac{10}{7}\)\(x\) (\(x\) \(\in\) N)
\(\left(\dfrac{20}{14}\right)^x\) = \(\dfrac{10}{7}\)⇒ \(x\)\(\left(\dfrac{10}{7}\right)^x\) = \(\dfrac{10}{7}\)\(x\)
\(x\) = \(\left(\dfrac{10}{7}\right)^x\): \(\dfrac{10}{7}\) ⇒ \(x\) =\(\left(\dfrac{10}{7}\right)^{x-1}\)
Nếu \(x\) = 0 ta có 0 = (\(\dfrac{10}{7}\))-1 = \(\dfrac{7}{10}\) (vô lý)
Nếu \(x\) = 1 ta có: 1 = \(\left(\dfrac{10}{7}\right)^{1-1}\) = 1 (nhận)
Nếu \(x\) > 1 ta có: \(x\) \(\in\) N mà (\(\dfrac{10}{7}\))\(x\) không phải là số tự nhiên nên
\(x\) \(\ne\) (\(\dfrac{10}{7}\))\(x-1\) (loại)
Từ những lập luận trên ta có \(x\) = 1 là số tự nhiên duy nhất thỏa mãn đề bài.
Vậy \(x\) = 1
19 tháng 9 2021
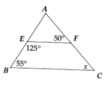
Ta có \(\widehat{FEB}+\widehat{EBC}=125^0+55^0=180^0\)
Mà 2 góc này ở vị trí trong cùng phía nên \(EF//BC\)
Do đó \(\widehat{AFE}=\widehat{ACB}=50^0\)(2 góc đồng vị)
\(\Rightarrow x=\widehat{ACB}=50^0\)
4 tháng 9 2018
( 4,82 - 14,4 : 1,2 + 3,1 ) . 0,5 - [ 2,9 . 4,2 - 4,5 : ( -0,5 ) + 13,22 ]
= ( 4,82 - 12 + 3,1 ) . 0,5 - [ 12,18 - ( -9 ) + 13,22 ]
= ( -7,18 + 3,1 ) . 0,5 - [ 21,18 + 13,22 ]
= ( -4,08) . 0,5 - 34,4
= ( -2,04 ) - 34,4
= ( -36,44 )
Hk tốt
18 tháng 9 2021
Xét tam giác ABC có:
\(\widehat{BEF}+\widehat{EBC}=125^0+55^0=180^0\)
Mà 2 góc này là 2 góc kề bù
=> EF//BC
=> \(\widehat{AFE}=\widehat{ACB}\)(2 góc đồng vị)
\(\Rightarrow x=50^0\)
12 tháng 6 2017
Giả thiết aÔd + cÔb = 200o
Mà aÔd = cÔb [đối đỉnh]
=> aÔd = cÔb = 200o/2 = 100o
Vì aÔd + dÔb = 180o [kề bù]
=> dÔb = 180o - 100o = 80o
=> dÔb = aÔc = 80o [đối đỉnh]
G
8 tháng 11 2017
Không được k 3 lần đâu, bạn làm kiểu gì, hay là bạn bảo thế xong rồi lúc có người giải rồi bạn lại bảo:" Xin lỗi bạn, Online Math không cho phép k 3 lần, mình chỉ k được một lần thôi, thông cảm cho mình nhé ...".
THÔI ĐI!?
KHÔNG AI TIN LÀ BẠN K CHO 3 LẦN ĐÂU, MÌNH NGHĨ BẠN NÊN NÓI THẬT THÌ TỐT HƠN ĐÓ !!?
Vì M = Q = \(90^o\) => M+N=\(180^o\) (trong cùng phía)
=> MN//QP
N+P=\(180^o\)(trong cùng phía)
=> x=P= \(180^o\)-\(135^o\)=\(45^o\)
Vậy x= \(45^o\)
Ta có: MN//QP
nên \(x+135^0=180^0\)
hay \(x=45^0\)