K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VM
0
9 tháng 9 2017
a/ \(27^x.9^x=9^{27}:81\)
\(\Leftrightarrow3^{3x}.3^{2x}=3^{54}:3^4\)
\(\Leftrightarrow3^{2x+3x}=3^{50}\)
\(\Leftrightarrow2x+3x=50\)
\(\Leftrightarrow5x=50\)
\(\Leftrightarrow x=10\)
Vậy ...
C
9 tháng 9 2017
\(a.27^x.9^x=9^{27}:81\)
\(\left(3^3\right)^x.\left(3^2\right)^x=\left(3^2\right)^{27}:\left(3^2\right)^2\)
\(3^{3x}.3^{2x}=3^{50}\)
\(3^{3x+2x}=3^{50}\)
\(\Rightarrow3x+2x=50\)
\(x\left(3+2\right)=50\)
\(x=50:5=10\)
Vậy\(x=10\)
\(b.\left(\dfrac{12}{25}\right)^x=\left(\dfrac{5}{3}\right)^{-2}-\left(-\dfrac{3}{5}\right)^4\)
\(\left(\dfrac{12}{25}\right)^x=\dfrac{9}{25}-\dfrac{81}{625}\)
\(\left(\dfrac{12}{25}\right)^x=\dfrac{144}{625}\)( Đề sai )
HP
1
VM
8 tháng 9 2019
a) \(5^n.25=125^2\)
\(\Rightarrow5^n.5^2=\left(5^3\right)^2\)
\(\Rightarrow5^n.5^2=5^6\)
\(\Rightarrow5^n=5^6:5^2\)
\(\Rightarrow5^n=5^4\)
\(\Rightarrow n=4\)
Vậy \(n=4.\)
b) \(3^n.9^2=27^3\)
\(\Rightarrow3^n.\left(3^2\right)^2=\left(3^3\right)^3\)
\(\Rightarrow3^n.3^4=3^9\)
\(\Rightarrow3^n=3^9:3^4\)
\(\Rightarrow3^n=3^5\)
\(\Rightarrow n=5\)
Vậy \(n=5.\)
c) \(2^4.4^n=8^6\)
\(\Rightarrow\left(2^2\right)^2.4^n=2^{18}\)
\(\Rightarrow4^2.4^n=\left(2^2\right)^9\)
\(\Rightarrow4^2.4^n=4^9\)
\(\Rightarrow4^n=4^9:4^2\)
\(\Rightarrow4^n=4^7\)
\(\Rightarrow n=7\)
Vậy \(n=7.\)
Chúc bạn học tốt!
NT
0
D
18 tháng 5 2016
1.a) \(\left(\frac{3}{5}\right)^{15}:\left(\frac{9}{25}\right)^5=\frac{3^{15}}{5^{15}}.\frac{5^{10}}{3^{10}}=\frac{3^5}{5^5}=\left(\frac{3}{5}\right)^5\)
b)\(\left(\frac{2}{3}\right)^{10}:\left(\frac{4}{9}\right)^4=\frac{2^{10}}{3^{10}}.\frac{3^8}{2^8}=\frac{2^2}{3^2}=\left(\frac{2}{3}\right)^2\)
2.
a)\(2^x=4\Rightarrow2^x=2^2\Rightarrow x=2\)
b)\(x^3=-27\Rightarrow x^3=-3^3\Rightarrow x=-3\)
c)\(x^2=16\Rightarrow x=\pm4\)
d)\(\left(x+1\right)^2=9\Rightarrow\hept{\begin{cases}x+1=3\Rightarrow x=2\\x+1=-3\Rightarrow x=-4\end{cases}}\)
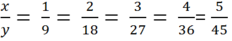
\(\Leftrightarrow3^x\cdot82=3^{50}+3^{54}\)
hay x=50