Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta=1-4\left(m+1\right)>0\Rightarrow m< -\dfrac{3}{4}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1^2+x_1x_2+3x_2=7\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)+3x_2=7\)
\(\Leftrightarrow x_1+3x_2=7\)
Kết hợp Viet ta được: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1+3x_2=7\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-2\\x_2=3\end{matrix}\right.\)
Thế vào \(x_1x_2=m+1\)
\(\Rightarrow m+1=-6\Rightarrow m=-7\)

\(F=x_1^2-3x_2-2013\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-7\end{matrix}\right.\)
Vì \(x_1\) là nghiệm của PT nên \(x_1^2+3x_1-7=0\Leftrightarrow x_1^2=7-3x_1\)
\(\Leftrightarrow F=7-3x_1-3x_2-2013\\ F=-2006-3\left(x_1+x_2\right)=-2006-3\left(-3\right)=-1997\)

Vì \(x_1\) là nghiệm PT nên \(x_1^2+3x_1-7=0\Leftrightarrow x_1^2=7-3x_1\)
\(F=x_1^2-3x_2-2013=7-3x_1-3x_2-2013\\ F=-3\left(x_1+x_2\right)-2006\)
Mà theo Viét ta có \(x_1+x_2=-3\)
\(\Rightarrow F=\left(-3\right)\left(-3\right)-2006=-1997\)

\(\Delta'=1-4\left(m+1\right)=-4m-3>0\Rightarrow m< -\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1^2+x_1x_2=7-3x_2\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)=7-3x_2\)
\(\Leftrightarrow x_1=7-3x_2\)
\(\Leftrightarrow x_1+x_2=7-2x_2\)
\(\Leftrightarrow1=7-2x_2\Rightarrow x_2=3\Rightarrow x_1=1-x_2=-2\)
Thế vào \(x_1x_2=m+1\Rightarrow-6=m+1\Rightarrow m=-7\)

\(x^2 - 4x - 3 = 0\) có 1.(-3) < 0
=> Phương trình có hai nghiệm phân biệt
Áp dụng hệ thức Vi-et có \(x_1 + x_2 = 4\) \(; x_1x_2 = -3\)
Mà \(A = \dfrac{x_1^2}{x_2} + \dfrac{x_2^2}{x_1}\)
\(= \dfrac{x_1^3 + x_2^3}{x_1x_2}\)
\(= \dfrac{(x_1 + x_2)(x_1^2 - x_1x_2 + x_2^2)}{x_1x_2}\)
\(=\dfrac{(x_1+x_2)[(x_1 +x_2)^2 - 3x_1x_2]}{x_1x_2}\)
\(=\dfrac{4.[4^2 - 3.(-3)]}{-3}\)
\(= \dfrac{-100}{3}\)

Lời giải:
Theo định lý Viet:
$x_1+x_2=2$
$x_1x_2=-6$
Khi đó:
$A=2x_1-x_1x_2+2x_2=2(x_1+x_2)-x_1x_2$
$=2.2-(-6)=4+6=10$

a, \(\Delta'=\left(-m\right)^2-1\left(-1\right)=m^2+1>0\)
Vậy phương trình đã cho luôn có hai nghiệm phân biệt x1 và x2
b, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-1\end{matrix}\right.\)
\(x^2_1+x^2_2-x_1x_2=7\\ \Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=7\\ \Leftrightarrow\left(2m\right)^2-3\left(-1\right)=7\\ \Leftrightarrow4m^2+3=7\\ \Leftrightarrow4m^2=4\\ \Leftrightarrow m^2=1\\ \Leftrightarrow m=\pm1\)
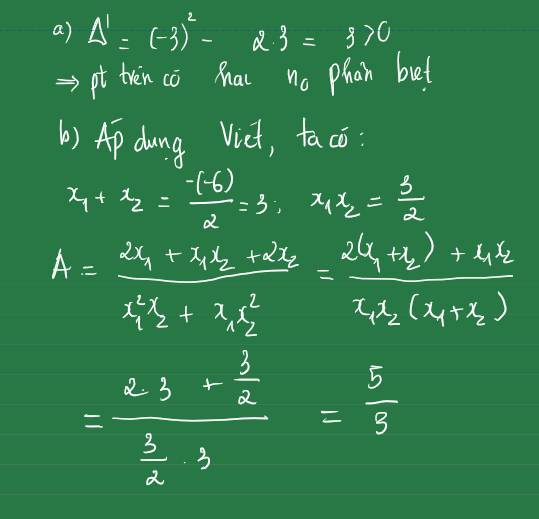
a) Do a = 3; c = -7 nên a và c trái dấu
Vậy phương trình luôn có hai nghiệm phân biệt
b) Theo Viét ta có:
x₁ + x₂ = -4/3
x₁x₂ = -7/3
Ta có:
2x₁ - (x₁ - x₂ - x₁x₂)
= 2x₁ - x₁ + x₂ + x₁x₂
= x₁ + x₂ + x₁x₂
= -4/3 - 7/3
= -11/3
\(3x^2+4x-7=0\)
\(a,\) Để pt có 2 nghiệm phân biệt thì \(\Delta>0\Rightarrow4^2-4.3.\left(-7\right)=100>0\)
Vậy pt có 2 nghiệm phân biệt \(x_1,x_2\)
\(b,\)Theo Vi-ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{4}{3}\\x_1x_2=\dfrac{c}{a}=-\dfrac{7}{3}\end{matrix}\right.\)
Ta có : \(2x_1-\left(x_1-x_2-x_1x_2\right)\)
\(=2x_1-x_1+x_2-x_1x_2\)
\(=x_1+x_2-x_1x_2\)
\(=-\dfrac{4}{3}-\left(-\dfrac{7}{3}\right)\)
\(=-\dfrac{4}{3}+\dfrac{7}{3}\)
\(=\dfrac{3}{3}=1\)
Vậy giá trị của biểu thức là \(1\)