Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Có bao nhiêu giá trị nguyên của m để pt sin2 x - sinx - 3 -m = 0 có nghiệm duy nhất thuộc [-π/2;π/2]


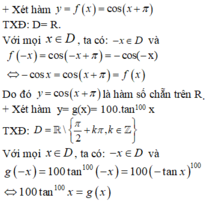
Do đó: y= 100 tan100x là hàm chẵn trên tập xác định của nó.
Đáp án B

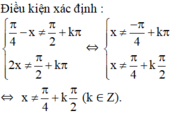
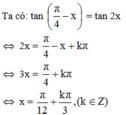
Kết hợp với điều kiện xác định suy ra
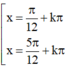 (k ∈ Z)
(k ∈ Z)
Vậy với 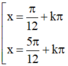 (k ∈ Z)
(k ∈ Z)
thì 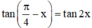

+ Xét hàm y = f x = cos x + π
TXĐ: D= R
Với mọi x ∈ D , ta có: − x ∈ D và
f − x = cos − x + π = − cos x = cos x + π = f x
Do đó y = cos x + π là hàm số chẵn trên R.
+ Xét hàm y = g x = tan 2016 x
TXĐ: D = ℝ \ π 2 + k π , k ∈ ℤ
Với mọi x ∈ D , ta có: − x ∈ D và
g − x = tan 2016 − x = − tan x 2016 = tan 2016 x = g x
Do đó: y = tan 2016 x là hàm chẵn trên tập xác định của nó
Chọn đáp án B.

y = \(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\)
y = \(\dfrac{sin^2x}{sinx.cosx-cos^2x}+\dfrac{1}{4}=\dfrac{\dfrac{sin^2x}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}-1}+\dfrac{1}{4}\)
y = \(\dfrac{tan^2x}{tanx-1}+\dfrac{1}{4}\)
y = \(\dfrac{4tan^2x+tanx-1}{4tanx-4}\). Đặt t = tanx. Do x ∈ \(\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\) nên t ∈ (1 ; +\(\infty\))\
Ta đươc hàm số f(t) = \(\dfrac{4t^2+t-1}{4t-4}\)
⇒ ymin = \(\dfrac{17}{4}\) khi t = 2. hay x = arctan(2) + kπ
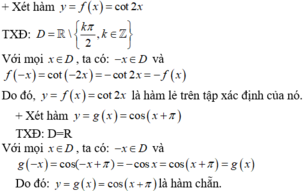
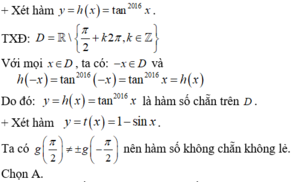
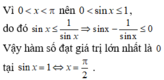
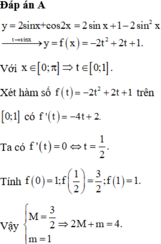
27.
\(\cos\left(\frac{\pi}{6}-2x\right)=\sin x\)
\(\Leftrightarrow\sin\left(\frac{\pi}{2}-\frac{\pi}{6}+2x\right)=\sin x\)
\(\Leftrightarrow\sin\left(\frac{\pi}{3}+2x\right)=\sin x\)
\(\Leftrightarrow\frac{\pi}{3}+2x=\pi-x+k2\pi\Leftrightarrow x=\frac{2}{9}\pi+\frac{2}{3}k\pi\)
\(\frac{\pi}{2}< \frac{2}{9}\pi+\frac{2}{3}k\pi< \pi\Leftrightarrow\frac{5}{18}\pi< \frac{2}{3}k\pi< \frac{7}{9}\pi\)
\(\Leftrightarrow\frac{5}{12}< k< \frac{7}{6}\Rightarrow k=1\)
Vậy phương trình có 1 nghiệm thuộc khoảng \(\left(\frac{\pi}{2};\pi\right)\)
19. \(\sin3x=\sin x\Leftrightarrow3x=\pi-x+k2\pi\Rightarrow x=\frac{\pi}{4}+\frac{1}{2}k\pi\)
33. \(DKXD:\left\{{}\begin{matrix}\cos3x\ne0\\\sin2x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x\ne\frac{\pi}{2}+k\pi\\2x\ne\pi+k\pi\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\frac{\pi}{6}+\frac{1}{3}k\pi\\x\ne\frac{\pi}{2}+\frac{1}{2}k\pi\end{matrix}\right.\)
\(\tan3x.\cot2x=1\Leftrightarrow\tan3x=\frac{1}{\cot2x}=\tan2x\)
\(\Leftrightarrow3x=\pi+2x+k\pi\Leftrightarrow x=\pi+k\pi\) (t/m)