Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d: \(=\sqrt{5}\left(\sqrt{3}-1\right)-\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}\)
=căn 5-1/2*căn 5
=1/2*căn 5
e: \(=\dfrac{2\left(\sqrt{8}-\sqrt{3}\right)}{\sqrt{6}\left(\sqrt{3}-\sqrt{8}\right)}-\dfrac{1}{\sqrt{6}}=\dfrac{2}{\sqrt{6}}-\dfrac{1}{\sqrt{6}}=\dfrac{1}{\sqrt{6}}\)
f:=2+căn 3+căn 2-2-căn 3=căn 2

`(5sqrt{1/5}+1/2sqrt{20}-5/4sqrt{4/5}+sqrt{5}):2/5
`=(sqrt5+1/2*2sqrt5-sqrt{5/4}+sqrt5):2/5`
`=(sqrt5+sqrt5+sqrt5-sqrt5/2):2/5`
`=(5/2*sqrt5):2/5`
`=25/4sqrt5`
`1/3sqrt{48}+3sqrt{75}-sqrt{27}-10sqrt{1 1/3}`
`=1/3*4sqrt3+3*5sqrt3-3sqrt3-10sqrt{4/3}`
`=4/sqrt3+15sqrt3-3sqrt3-20/sqrt3`
`=12sqrt3-16/sqrt3`

a: \(=2\sqrt{5}-5\sqrt{5}-4\sqrt{5}+11\sqrt{5}=4\sqrt{5}\)
b: \(=2\sqrt{5}-2-2\sqrt{5}=-2\)
c: \(=3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
d: \(=\dfrac{2\left(2\sqrt{2}-\sqrt{3}\right)}{\sqrt{6}\left(\sqrt{3}-2\sqrt{2}\right)}-\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{-3}{\sqrt{6}}=-\dfrac{3\sqrt{6}}{6}=-\dfrac{\sqrt{6}}{2}\)
e: \(=\dfrac{8}{3}\sqrt{3}-\dfrac{1}{3}\sqrt{3}-\dfrac{4}{5}\sqrt{3}=\dfrac{23}{15}\sqrt{3}\)

Bài 1:
a) Ta có: \(\left(5\sqrt{\dfrac{1}{5}}+\dfrac{1}{2}\sqrt{20}-\dfrac{5}{4}\sqrt{\dfrac{4}{5}}+\sqrt{5}\right)\)
\(=\left(\sqrt{5}+\sqrt{5}-\dfrac{5}{4}\cdot\dfrac{2}{\sqrt{5}}+\sqrt{5}\right)\)
\(=3\sqrt{5}-\dfrac{1}{2}\sqrt{5}\)
\(=\dfrac{5}{2}\sqrt{5}\)
c) Ta có: \(\dfrac{5\sqrt{7}-7\sqrt{5}+2\sqrt{70}}{\sqrt{35}}\)
\(=\dfrac{\sqrt{35}\left(\sqrt{5}-\sqrt{7}+2\sqrt{2}\right)}{\sqrt{35}}\)
\(=2\sqrt{2}+\sqrt{5}-\sqrt{7}\)
Bài 2:
e) ĐKXĐ: \(\dfrac{4}{3}\le x\le6\)
Ta có: \(\sqrt{6-x}=3x-4\)
\(\Leftrightarrow6-x=\left(3x-4\right)^2\)
\(\Leftrightarrow9x^2-24x+16+6-x=0\)
\(\Leftrightarrow9x^2-25x+22=0\)
\(\Delta=\left(-25\right)^2-4\cdot9\cdot22=625-792< 0\)
Vậy: Phương trình vô nghiệm

a. ĐKXĐ: $x\geq 0$
PT $\Leftrightarrow -5x-5\sqrt{x}+12\sqrt{x}+12=0$
$\Leftrightarrow -5\sqrt{x}(\sqrt{x}+1)+12(\sqrt{x}+1)=0$
$\Leftrightarrow (\sqrt{x}+1)(12-5\sqrt{x})=0$
Dễ thấy $\sqrt{x}+1>1$ với mọi $x\geq 0$ nên $12-5\sqrt{x}=0$
$\Leftrightarrow \sqrt{x}=\frac{12}{5}$
$\Leftrightarrow x=5,76$ (thỏa mãn)
b. ĐKXĐ: $x^2\geq 5$
PT $\Leftrightarrow \frac{1}{3}\sqrt{4}.\sqrt{x^2-5}+2\sqrt{\frac{1}{9}}\sqrt{x^2-5}-3\sqrt{x^2-5}=0$
$\Leftrightarrow \frac{2}{3}\sqrt{x^2-5}+\frac{2}{3}\sqrt{x^2-5}-3\sqrt{x^2-5}=0$
$\Leftrightarrow -\frac{5}{3}\sqrt{x^2-5}=0$
$\Leftrightarrow \sqrt{x^2-5}=0$
$\Leftrightarrow x=\pm \sqrt{5}$

a) \(E=2\sqrt{40\sqrt{12}}+3\sqrt{5\sqrt{48}}-2\sqrt{\sqrt{75}}-4\sqrt{15\sqrt{27}}.\)
\(=8\sqrt{5\sqrt{3}}+6\sqrt{5\sqrt{3}}-2\sqrt{5\sqrt{3}-12\sqrt{5\sqrt{3}}}\)
\(=0\)
b) \(F=\frac{1}{\sqrt{3}}+\frac{1}{3\sqrt{2}}+\frac{1}{\sqrt{3}}\sqrt{\frac{5}{12}-\frac{1}{\sqrt{6}}}.\)
Vì \(=\frac{5}{12}-\frac{1}{\sqrt{6}}=\frac{5-2\sqrt{6}}{12}=\frac{\left(\sqrt{3}-\sqrt{2}\right)^2}{12}\)
\(\frac{1}{\sqrt{3}}+\frac{1}{2\sqrt{3}}=\frac{\sqrt{3}}{3}+\frac{\sqrt{2}}{6}=\frac{2\sqrt{3}+\sqrt{2}}{6}\)
Nên \(F=\frac{2\sqrt{3}+\sqrt{2}}{6}+\frac{1}{\sqrt{3}}\sqrt{\frac{\left(\sqrt{3}-\sqrt{2}\right)^2}{12}}=\frac{2\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}}{6}=\frac{3\sqrt{3}}{6}=\frac{\sqrt{3}}{2}\)

Bài 2:
a)\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: \(x\ge2\))
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+\dfrac{6}{\sqrt{81}}\sqrt{x-2}=-4\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\Leftrightarrow-\sqrt{x-2}=-4\) \(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\) (thỏa)
Vậy...
b)\(\sqrt{9x^2+12x+4}=4x\)(Đk:\(9x^2+12x+4\ge0\))
\(\Leftrightarrow\left\{{}\begin{matrix}4x\ge0\\9x^2+12x+4=16x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+12x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+14x-2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-2\right)\left(-7x-2\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{7}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=2\) (tm đk)
Vậy...
c) \(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}\) (đk: \(x\ge1\))
\(\Leftrightarrow x-2\sqrt{x-1}=x-1\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{1}{2}\) \(\Leftrightarrow x=\dfrac{5}{4}\) (tm)
Vậy...

\(a) \sqrt{4x^2− 9} = 2\sqrt{x + 3}\)
\(ĐK:x\ge\dfrac{3}{2}\)
\(pt\Leftrightarrow4x^2-9=4\left(x+3\right)\)
\(\Leftrightarrow4x^2-9=4x+12\)
\(\Leftrightarrow4x^2-4x-21=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{22}}{2}\left(l\right)\\x=\dfrac{1+\sqrt{22}}{2}\left(tm\right)\end{matrix}\right.\)
\(b)\sqrt{4x-20}+3.\sqrt{\dfrac{x-5}{9}}-\dfrac{1}{3}\sqrt{9x-45}=4\)
\(ĐK:x\ge5\)
\(pt\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)
\(\Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\)
\(\Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)
\(c)\dfrac{2}{3}\sqrt{9x-9}-\dfrac{1}{4}\sqrt{16x-16}+27.\sqrt{\dfrac{x-1}{81}}=4\)
ĐK:x>=1
\(pt\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\)
\(\Leftrightarrow4\sqrt{x-1}=4\Leftrightarrow\sqrt{x-1}=1\)
\(\Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\)
\(d)5\sqrt{\dfrac{9x-27}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)
\(ĐK:x\ge3\)
\(pt\Leftrightarrow3\sqrt{x-3}-\dfrac{14}{3}\sqrt{x-3}-7\sqrt{x^2-9}+6\sqrt{x^2-9}=0\)
\(\Leftrightarrow-\dfrac{5}{3}\sqrt{x-3}-\sqrt{x^2-9}=0\Leftrightarrow\dfrac{5}{3}\sqrt{x-3}+\sqrt{x^2-9}=0\)
\(\Leftrightarrow(\dfrac{5}{3}+\sqrt{x+3})\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}=0\) (vì \(\dfrac{5}{3}+\sqrt{x+3}>0\))
\(\Leftrightarrow x-3=0\Leftrightarrow x=3\left(nhận\right)\)

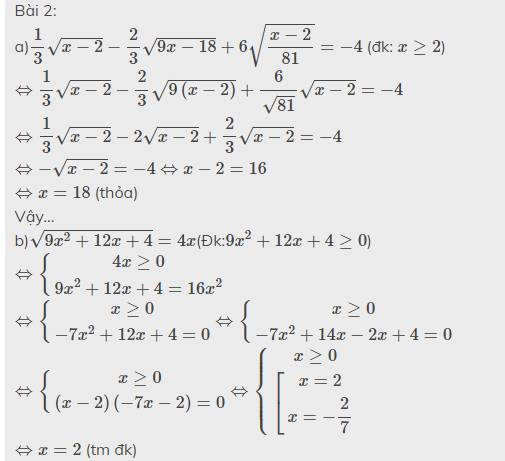
\(1,=2\sqrt{3}-3\sqrt{3}+4\sqrt{3}=3\sqrt{3}\\ 2,=\left(2\sqrt{6}+2\sqrt{5}-4\sqrt{5}\right):5=\dfrac{2\sqrt{6}}{5}-\dfrac{2\sqrt{5}}{5}\\ 3,=6\sqrt{3}-\dfrac{4\sqrt{3}}{3}-4\sqrt{3}-\dfrac{5\sqrt{3}}{3}=2\sqrt{3}-\dfrac{9\sqrt{3}}{3}=2\sqrt{3}-3\sqrt{3}=-\sqrt{3}\\ 4,Sửa:\dfrac{1}{\sqrt{5}-\sqrt{3}}-\dfrac{1}{\sqrt{5}+\sqrt{3}}\\ =\dfrac{\sqrt{5}+\sqrt{3}-\sqrt{5}+\sqrt{3}}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\)
1) \(=2\sqrt{3}-3\sqrt{3}+4\sqrt{3}=3\sqrt{3}\)
2) \(=\left(2\sqrt{6}+2\sqrt{5}-4\sqrt{5}\right)=\dfrac{2\sqrt{6}}{5}+\dfrac{2\sqrt{5}}{5}-\dfrac{4\sqrt{5}}{5}\)
3) \(=6\sqrt{3}-\dfrac{4\sqrt{3}}{3}-4\sqrt{3}-\dfrac{5\sqrt{3}}{3}=2\sqrt{3}-3\sqrt{3}=-\sqrt{3}\)
4) \(=\dfrac{\sqrt{5}+\sqrt{3}-\sqrt{5}+\sqrt{3}}{5-3}=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\)