Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nửa chu vi miếng đất hình chữ nhật là:
Gọi chiều dài miếng đất là:
chiều rộng miếng đất là:
Miếng đất hình chữ nhật có nửa chu vi là .
⇒ Phương trình:
5 lần chiều rộng hơn 2 lần chiều dài 40m.
⇒ Phương trình:
Từ và ta có hệ phương trình:
⇔
⇔
⇔
⇔
⇔
⇔
Vậy miếng đất hình chữ nhật có chiều dài là và chiều rộng .

a) (d) cắt (P) tại A => A thuộc d và (P)
xA= 3; A \(\in\) d=> yA = -xA - \(\frac{3}{2}\) => yA = -3 - \(\frac{3}{2}\) = \(\frac{-9}{2}\)
Mặt khác, A \(\in\) (P) => yA = axA2 => \(\frac{-9}{2}\) = a. 32 => a = \(\frac{-9}{2}\): 9 = \(\frac{-1}{2}\)
Vậy (P) có dạng y = \(\frac{-1}{2}\).x2
+) Vẽ đồ thị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -2 | \(\frac{-1}{2}\) | 0 | \(\frac{-1}{2}\) | -2 |
(P) đí qua 4 điểm (-2;-2); (-1;\(\frac{-1}{2}\)); (0;0); (1;\(\frac{-1}{2}\)); (2;-2)
b) Phương trình hoành độ giao điểm: \(\frac{-1}{2}\).x2 = - x - \(\frac{3}{2}\)
<=> -x2 + 2x + 3 = 0
<=> x = -1 hoặc x = 3 (Vì a - b + c = -1 - 2 + 3 = 0)
=> xB = -1 => yB = \(\frac{-1}{2}\).(-1)2 = \(\frac{-1}{2}\)
Vậy B (-1;\(\frac{-1}{2}\))

a: 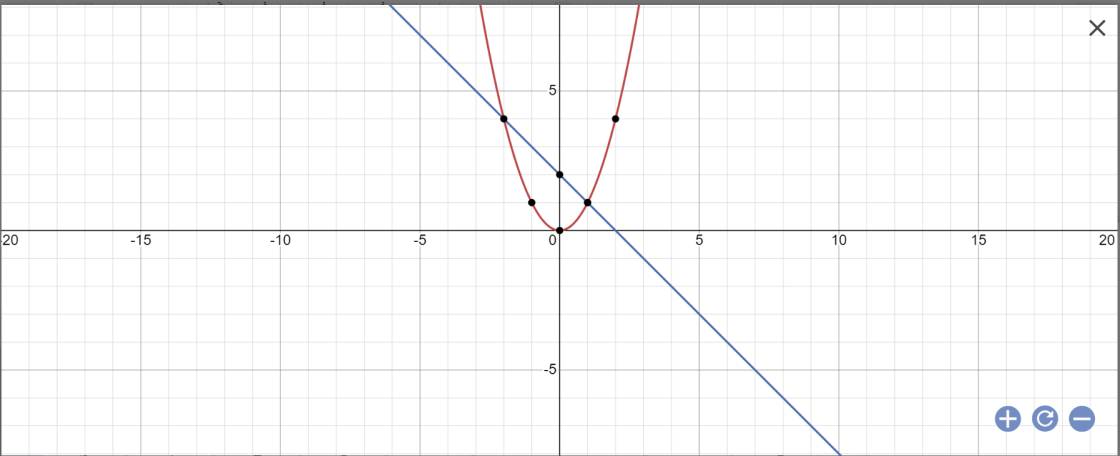
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

1: Để (d)//(d') thì \(\left\{{}\begin{matrix}m-3=1\\2\ne-5\left(đúng\right)\end{matrix}\right.\)
=>m-3=1
=>m=4
Thay m=4 vào (d), ta được:
\(y=\left(4-3\right)x+2=x+2\)
Vẽ đồ thị:
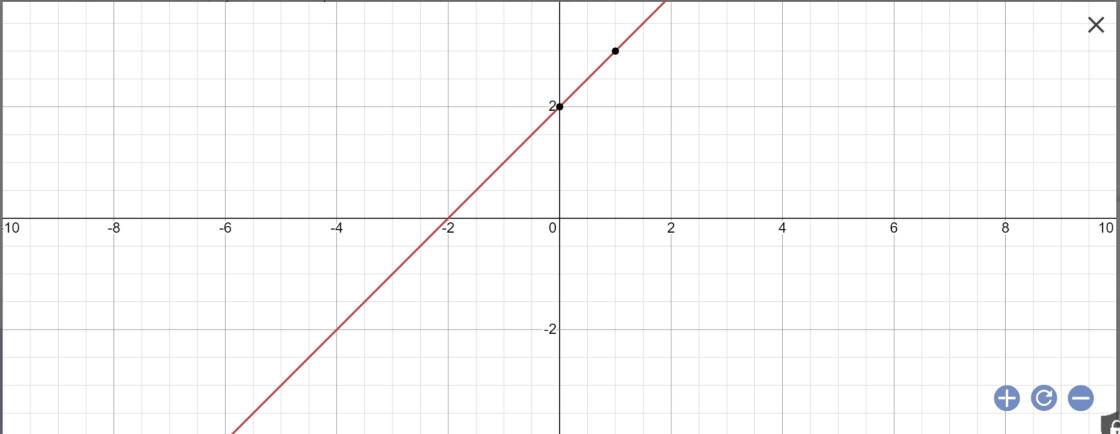
2: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(m-3\right)x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x\left(m-3\right)=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{2}{m-3}\\y=0\end{matrix}\right.\)
Vậy: \(A\left(-\dfrac{2}{m-3};0\right)\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m-3\right)\cdot x+2=0\left(m-3\right)+2=2\end{matrix}\right.\)
vậy: B(0;2)
\(OA=\sqrt{\left(-\dfrac{2}{m-3}-0\right)^2+\left(0-0\right)^2}\)
\(=\sqrt{\left(-\dfrac{2}{m-3}\right)^2+0^2}=\dfrac{2}{\left|m-3\right|}\)
\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=2\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OBA}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot2\cdot\dfrac{2}{\left|m-3\right|}=\dfrac{2}{\left|m-3\right|}\)
Để \(S_{OAB}=2\) thì \(\dfrac{2}{\left|m-3\right|}=2\)
=>|m-3|=1
=>\(\left[{}\begin{matrix}m-3=1\\m-3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=4\\m=2\end{matrix}\right.\)
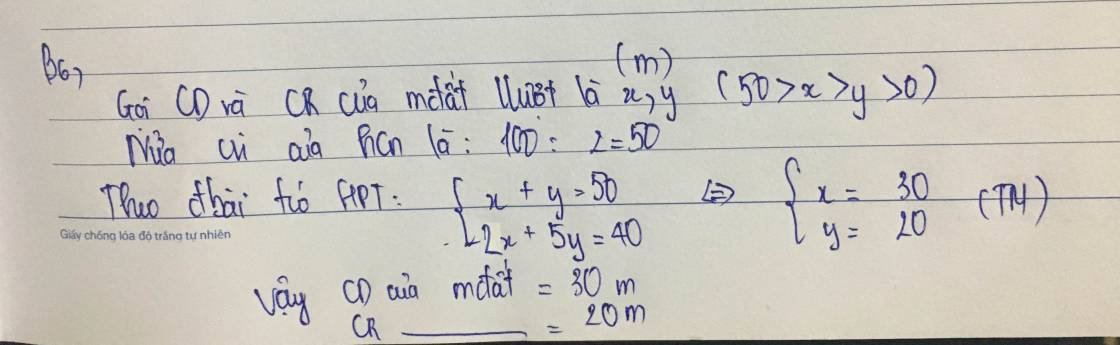
Bài 1
Gọi a (m) là chiều dài mảnh đất (0<a<100), b (m) là chiều rộng của mảnh đất (0<b<100)
Nửa chu vi mảnh đất: a+ b = 50 (1)
Theo đề bài ta có: 5b - 2a=40 (2)
Từ (1) (2) suy ra hệ pt . Ta giải pt được a=30, b=20
Vậy: CR=20m, CD=30m.
làm giùm bài 2 đi