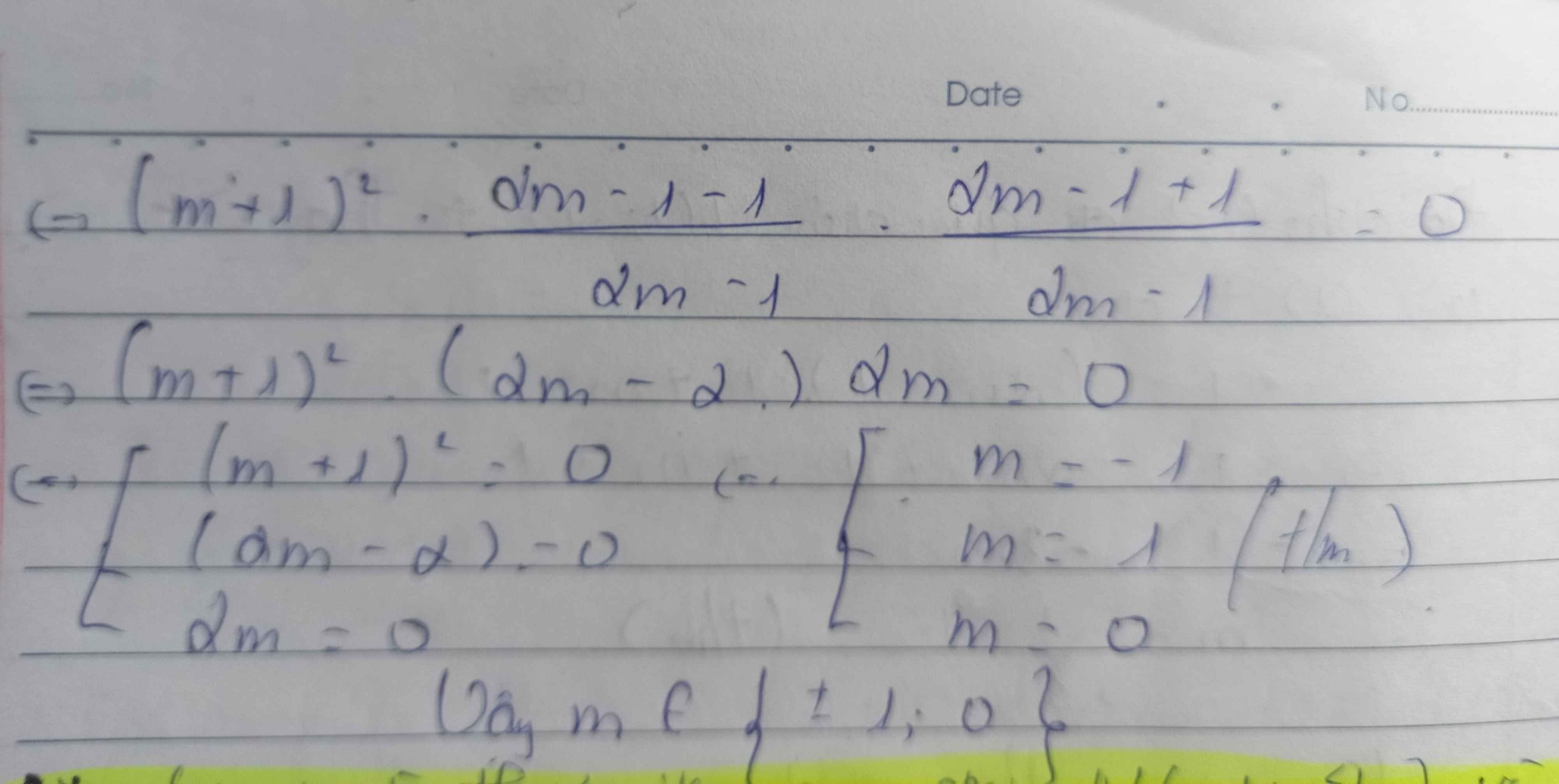Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. để hàm số đi qua M(-1,1) thì ta có
\(1=\left(2m-1\right)\times\left(-1\right)+m+1\Leftrightarrow m=1\)
b.Hàm số cắt trụ tung tại điểm \(A\left(0,m+1\right)\)
Hàm số cắt trục hoành tại điểm \(B\left(\frac{-m-1}{2m-1},0\right)\)
Để OAB là tam giác cân thì ta có \(OA=OB\ne0\Leftrightarrow\left|m+1\right|=\left|\frac{-m-1}{2m-1}\right|\ne0\)
\(\Leftrightarrow\left|2m-1\right|=1\Leftrightarrow\orbr{\begin{cases}m=0\\m=1\end{cases}}\)
a, Để đồ thị đi qua điểm M(-1;1) thì ta thay x = -1, y = 1 vào hàm số ta có:
\(1=\left(2m-1\right).\left(-1\right)+m+1\)
=>\(m=1\)
b,\(y=\left(2m-1\right)x+m+1\)
Cho \(x=0=>y=m+1=>OA=|m+1|\)
Cho \(y=0=>x=\frac{-m-1}{2m-1}=>B\left(\frac{-m-1}{2m-1};0\right)\)
\(=>OB=|\frac{-m-1}{2m-1}|=\frac{|m+1|}{|2m-1|}\)
\(\Delta AOB\)cân \(< =>\hept{\begin{cases}OA=OB\\OA>0\end{cases}}< =>\hept{\begin{cases}|m+1|\\|m+1|>0\end{cases}}\)
\(\hept{\begin{cases}|2m-1|\\m\ne-1\end{cases}< =>\hept{\begin{cases}2m-1=1\\2m-1=-1\end{cases}}}< =>\hept{\begin{cases}m=1\\m=0\end{cases}}\)
Vậy với m = 0 hoặc m = 1 thì đồ thị hàm số thỏa mãn yêu cầu của bài toán

a) Để đồ thị hàm số đi qua điểm A(-2;3), ta thay x = -2 và y = 3 vào phương trình hàm số:
3 = (2m+1)(-2) + 3m - 1
Giải phương trình, ta có:
3 = -4m - 2 + 3m - 1
3 = -m - 3
m = -6
b) Để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2, ta thay x = 2 vào phương trình hàm số:
0 = (2m+1)(2) + 3m - 1
Giải phương trình, ta có:
0 = 4m + 2 + 3m - 1
0 = 7m + 1
m = -1/7
c) Để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2, ta thay y = 2 vào phương trình hàm số:
2 = (2m+1)x + 3m - 1
2 = (2m+1)x + 3m - 1
(2m+1)x + 3m = 3
d) Để đồ thị hàm số cắt đường thẳng Y = x + 2 tại điểm có hoành độ bằng 3, ta thay x = 3 vào phương trình hàm số và đường thẳng:
(2m+1)(3) + 3m - 1 = 3 + 2
Giải phương trình, ta có:
6m + 4 = 5
m = 1/6
e) Để đồ thị hàm số cắt đường thẳng Y = -x - 3 tại điểm có tung độ bằng -1, ta thay y = -1 vào phương trình hàm số và đường thẳng:
-1 = (2m+1)x + 3m - 1 = -x - 3
(2m+1)x + 3m = -2
g) Để vẽ đồ thị hàm số khi m = 2, ta thay m = 2 vào phương trình hàm số:
Y = (2(2)+1)x + 3(2) - 1
Y = 5x + 5
a: Thay x=-2 và y=3 vào (d), ta được:
-2(2m+1)+3m-1=3
=>-4m-2+3m-1=3
=>-m-3=3
=>m+3=-3
=>m=-6
b: Thay x=2 và y=0 vào (d), ta được:
2(2m+1)+3m-1=0
=>7m+3=0
=>m=-3/7
c: Thay x=0 và y=2 vào (d), ta được:
0(2m+1)+3m-1=2
=>3m-1=2
=>m=1
d: Thay x=3 vào y=x+2, ta được:
y=3+2=5
Thay x=3; y=5 vào (d), ta được:
3(2m+1)+3m-1=5
=>9m+2=5
=>9m=3
=>m=1/3
e: Thay y=-1 vào y=-x-3, ta được:
-x-3=-1
=>x+3=1
=>x=-2
Thay x=-2 và y=-1 vào (d), ta được:
-2(2m+1)+3m-1=-1
=>-4m-2+3m-1=-1
=>-m-3=-1
=>-m=2
=>m=-2
g: Khi m=2 thì (d) sẽ là:
y=(2*2+1)x+3*2-1
=5x+5

a. Để đồ thị qua A
\(\Rightarrow-1=-3m+m-1\)
\(\Leftrightarrow m=0\)
b. Để đồ thị cắt trục tung tại điểm có tung độ 2
\(\Rightarrow m-1=2\)
\(\Leftrightarrow m=3\)
c. Để đồ thị cắt trục hoành tại điểm có hoành độ 3
\(\Rightarrow0=3m+m-1\)
\(\Leftrightarrow m=\dfrac{1}{4}\)

y=3x+b
a)Vì hàm số cắt trục tung tại điểm có tung độ = -2 nên x=0,y=-2
Thay x=0,y=-2 vào hàm số ta đc:
3.0+b=-2
\(\Rightarrow\)b=-2
b)Để đồ thị hàm số đi qua điểm M[ -2, 1] nên x=-2,y=1
2.(-2)+b=1\(\Rightarrow\)-4+b=1\(\Rightarrow\)b=5
c) thay x=3,y=x-2 ta đc :
y=1-2=-1
Thay x=1 và y=-1 vào y=3x+b ta đc
3.1+b=-1 \(\Rightarrow\)3+b=-1 \(\Rightarrow\)b=-4

a: Thay x=2 và y=0 vào y=(m+1)x-1, ta được:
2(m+1)-1=0
=>2(m+1)=1
=>m+1=1/2
=>\(m=\dfrac{1}{2}-1=-\dfrac{1}{2}\)
b: Thay x=0 và y=2 vào y=(m+1)x-1, ta được:
\(0\cdot\left(m+1\right)-1=2\)
=>-1=2(vô lý)

Lời giải:
PT hoành độ giao điểm:
$x^2-2mx-(2m+1)=0(*)$
Để (P) và (d) cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ thì PT $(*)$ phải có 2 nghiệm pb $x_1,x_2$
$\Leftrightarrow \Delta'=m^2+2m+1>0\Leftrightarrow (m+1)^2>0$
$\Leftrightarrow m\neq -1$
Áp dụng định lý Viet: $x_1+x_2=2m; x_1x_2=-(2m+1)$
Khi đó:
$\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1$
$\Leftrightarrow \sqrt{2m}+\sqrt{3-2m-1}=2m+1$
\(\Leftrightarrow \left\{\begin{matrix}
0\leq m< 1\\
\sqrt{2m}+\sqrt{2(1-m)}=2m+1\end{matrix}\right.\)
Bình phương 2 vế dễ dàng giải ra $m=\frac{1}{2}$ (thỏa)

Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)