
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{1}{\sqrt{25}+\sqrt{24}}+\dfrac{1}{\sqrt{24}+\sqrt{23}}+....+\dfrac{1}{\sqrt{2}+1}\)
\(A=\sqrt{25}-\sqrt{24}+\sqrt{24}-\sqrt{23}+......+\sqrt{2}-1=\sqrt{25}-1=4\)

Vẽ đồ thị hàm số:
1, y = 1/4x mũ 2
2, y = -1/4 x mũ 2
3, y = -2 x mũ 2
4, y = -1/2 x mũ 2
5, y = 3 x mũ 2


Lời giải:
a)
Ta có \(A=7.5^{2n}+12.6^n=7.25^n+12.6^n\)
Vì \(25\equiv 6\pmod {19}\Rightarrow 7.25^n\equiv 7.6^n\pmod {19}\)
Do đó \(A\equiv 7.6^n+12.6^n\equiv 19.6^n\equiv 0\pmod {19}\)
Ta có đpcm.
b) Đặt biểu thức là $B$ .
Dễ thấy \(1924,1920\vdots 4\Rightarrow B\vdots 4(1)\)
Có \(2003\equiv -7\pmod {30}\Rightarrow 2003^{2004^n}\equiv (-7)^{2004^n}\equiv 7^{2004^n}\pmod {30}\)
Mặt khác \(7^4\equiv 1\pmod {30}\) , \(2004^n\vdots 4\) nên \(7^{2004^n}\equiv 1\pmod {30}\)
Từ hai điều trên suy ra \(2003^{2004^n}\equiv 1\pmod {30}\) . Đặt \(2003^{2004^n}=30k+1\)
Khi đó \(1924^{2003^{2004^n}}+1920=1924^{30k+1}+1924\)
Vì \(UCLN(1924,31)=1\) nên áp dụng định lý Fermat nhỏ:
\(1924^{30}\equiv 1\pmod {31}\Rightarrow 1924^{30k}\equiv 1\pmod{31}\)
\(\Rightarrow 1924^{30k+1}\equiv 1924\pmod {31}\Rightarrow 1924^{30k+1}+1920\equiv 1924+1920\equiv 3844\equiv 0\pmod{31}\)
Do đó \(B\vdots 31\) \((2)\)
Từ \((1),(2)\) và \((31,4)=1\Rightarrow B\vdots (31.4=124)\)
c)
\(5^{2n+1}+2^{n+4}+2^{n+1}=5^{2n+1}+2^{n+1}(2^3+1)\)
\(=5^{2n+1}+18.2^n=5.25^n+18.2^n\)
\(\equiv 5.2^{n}+18.2^n\pmod {23}\)
\(\Leftrightarrow 5^{2n+1}+2^{n+4}+2^{n+1}\equiv 23.2^n\equiv 0\pmod {23}\)
Ta có đpcm.

-Xét \(x\ge y\ge z\). Dễ cm bđt đúng
-Xét \(x\ge z\ge y\)
Đặt x=z+a, z=y+b với \(a,b\ge0\)
=>x=y+a+b
BĐT\(< =>\frac{x-y}{y\left(y+1\right)}\ge\frac{x-z}{x\left(x+1\right)}+\frac{z-x}{z\left(z+1\right)}\)
<=>\(\frac{a+b}{y\left(y+1\right)}\ge\frac{a}{x\left(x+1\right)}+\frac{b}{z\left(z+1\right)}\)
Vì \(x\ge z\ge y=>x\left(x+1\right)\ge z\left(z+1\right)\ge y\left(y+1\right)\)
\(=>\frac{a}{y\left(y+1\right)}\ge\frac{a}{x\left(x+1\right)},\frac{b}{y\left(y+1\right)}\ge\frac{b}{z\left(z+1\right)}\)
=>\(\frac{a+b}{y\left(y+1\right)}\ge\frac{a}{x\left(x+1\right)}+\frac{b}{z\left(z+1\right)}\)=>bđt cần cm đúng=>đpcm

Ta có:
S = n n 4 + 5 n 3 + 5 n 2 − 5 n − 6 = n [ n 2 − 1 n 2 + 6 + 5 n n 2 − 1 ] = n ( n 2 − 1 ) ( n 2 + 5 n + 6 ) = n ( n − 1 ) ( n + 1 ) ( n + 2 ) ( n + 3 ) = ( n − 1 ) n ( n + 1 ) ( n + 2 ) ( n + 3 )
Ta có S là tích của 5 số nguyên tự nhiên liên tiếp chia hết cho 5! nên chia hết cho 120.
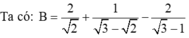
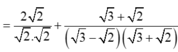
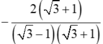
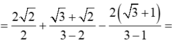

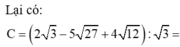
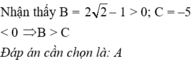
\(1+2+2^2+2^3+...+2^n=357680\)
\(\Leftrightarrow2\cdot\left(1+2+2^2+...+2^n\right)=2\cdot357680\)
\(\Leftrightarrow2+2^2+2^3+2^4+...+2^{n+1}=2\cdot357680\)
\(\Leftrightarrow\left(2+2^2+...+2^{n+1}\right)-\left(1+2+2^2+...+2^n\right)=2\cdot357680-357680\)
\(\Leftrightarrow\left(2-2\right)+\left(2^2-2^2\right)+...+\left(2^n-2^n\right)+\left(2^{n+1}-1\right)=357680\)
\(\Leftrightarrow2^{n+1}-1=357680\)
\(\Leftrightarrow2^{n+1}=357681\)
Xem lại đề
\(1+2+2^2+2^3+...+2^n=357680\)
\(\Rightarrow\dfrac{2^{n+1}-1}{2-1}=357680\)
\(\Rightarrow2^{n+1}=357680+1\)
\(\Rightarrow2^{n+1}=357681\Rightarrow n+1=\sqrt[]{357681}\Rightarrow n=\sqrt[]{357681}-1\)