Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Phương trình hoành độ giao điểm là:
3x-2=x-3
\(\Leftrightarrow2x=-1\)
hay \(x=-\dfrac{1}{2}\)
Thay \(x=-\dfrac{1}{2}\) vào y=x-3, ta được:
\(y=-\dfrac{1}{2}-3=\dfrac{-7}{2}\)

Lời giải:
a.
Đồ thị xanh lá là $y=-2x+3$, xanh nước biển là $y=\frac{1}{2}x$
b. PT hoành độ giao điểm:
$y=-2x+3=\frac{1}{2}x$
$\Leftrightarrow x=\frac{6}{5}$
$y=\frac{1}{2}.\frac{6}{5}=\frac{3}{5}$
Vậy tọa độ giao điểm là $(\frac{6}{5}, \frac{3}{5})$
c.
$Gọi ptđt có dạng $y=ax+b$
Vì $A,B\in (d)$ nên:
\(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3=4a+b\\ 2=-a+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{1}{5}\\ b=\frac{11}{5}\end{matrix}\right.\)
Vậy ptđt là $y=\frac{1}{5}x+\frac{11}{5}$

b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=-x+2\)
\(\Leftrightarrow x^2+x-2=0\)(1)
a=1; b=1; c=-2
Vì a+b+c=0 nên phương trình (1) có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{-2}{1}=-2\)
Thay x=1 vào (d), ta được:
y=-1+2=1
Thay x=-2 vào (d), ta được:
y=-(-2)+2=2+2=4
Vậy: (P) và (d) có hai tọa độ giao điểm là (1;1) và (-2;4)

b: Phương trình hoành độ giao điểm là:
2x+1=x+3
=>2x-x=3-1
=>x=2
Thay x=2 vào y=x+3, ta được:
y=2+3=5
a: 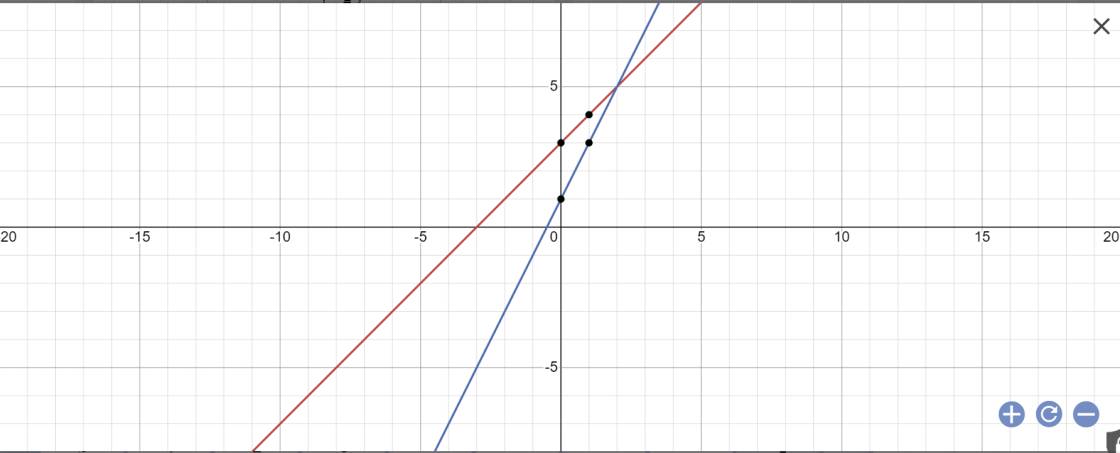

a) Bạn tự vẽ
b) Phương trình hoành độ giao điểm của (P) và (d)
\(x^2=-x+2\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
+) Với \(x=1\) thì \(y=1\)
+) Với \(x=-2\) thì \(y=4\)
Vậy (P) cắt (d) tại 2 điểm \(\left(1;1\right)\) và \(\left(-2;4\right)\)

a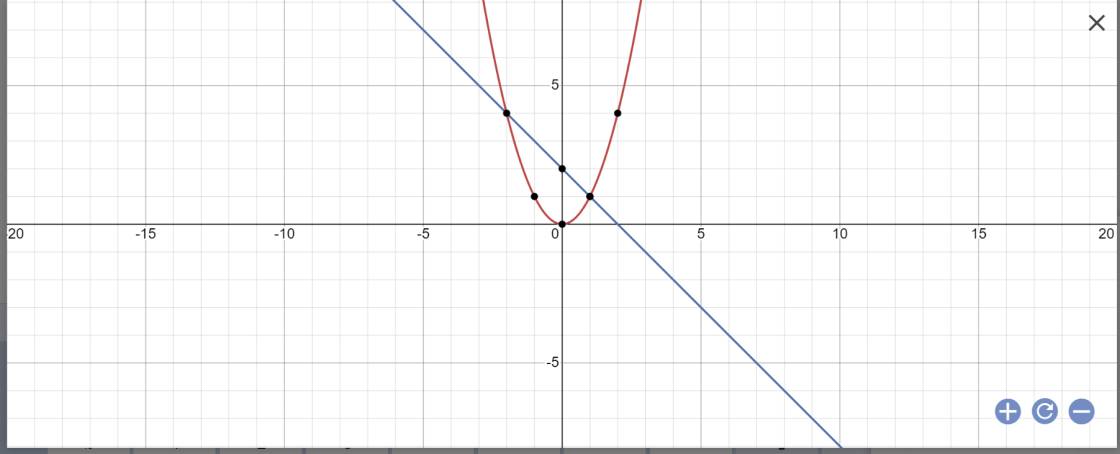
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

b) Phương trình hoành độ giao điểm là:
\(2x+6=-x+3\)
\(\Leftrightarrow2x+x=3-6\)
\(\Leftrightarrow3x=-3\)
hay x=-1
Thay x=-1 vào (d), ta được:
\(y=2\cdot\left(-1\right)+6=-2+6=4\)
Vậy: A(-1;4)

1:
a: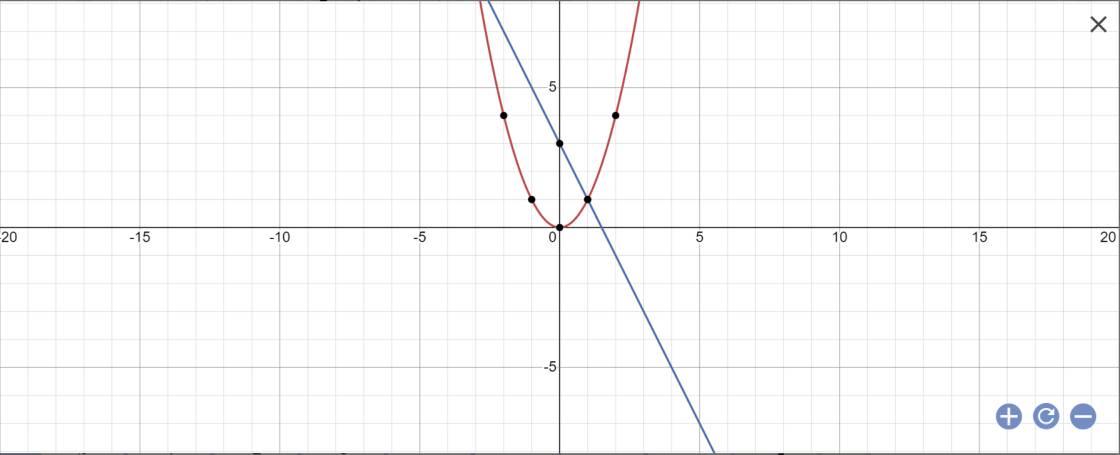
b: PTHĐGĐ là:
x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
=>y=9 hoặc y=1