Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số đó là x
Ta có phương trình: 10x+2=3.(200000+x)=>x=85714
Vậy số đó là 85714

Bài 1:
Số có 5 chữ số có dạng: \(\overline{abcde}\)
Khi viết thêm chữ số 2 vào đằng sau số đó ta được số mới là:
\(\overline{abcde2}\)
Khi viết thêm chữ số 2 vào đằng trước số đó ta được số mới là: \(\overline{2abcde}\)
Theo bài ra ta có: \(\overline{abcde2}\) = \(\overline{2abcde}\) \(\times\) 3
10\(\times\)\(\overline{abcde}\) + 2 = (200000 + \(\overline{abcde}\))\(\times\) 3
\(\overline{abcde}\) \(\times\)10 + 2 = 600000 + \(\overline{abcde}\)\(\times\) 3
\(\overline{abcde}\) \(\times\) 10 - \(\overline{abcde}\) \(\times\) 3 = 600000 - 2
\(\overline{abcde}\) \(\times\) ( 10 - 3) = 599998
7\(a\) = 599998
\(a\) = 599998: 7
\(a\) = 85714
Bài 2: Số có hai chữ số có dạng: \(\overline{ab}\)
Khi viết thêm chữ số 1 vào bên trái số và bên phải số đó ta có số mới là: \(\overline{1ab1}\)
Theo bài ra ta có: \(\overline{1ab1}\) = \(\overline{ab}\) \(\times\) 23
1001 + \(\overline{ab}\) \(\times\) 10 = \(\overline{ab}\) \(\times\) 23
\(\overline{ab}\) \(\times\) 23 - \(\overline{ab}\) \(\times\) 10 = 1001
\(\overline{ab}\) \(\times\)(23 - 10) = 1001
\(\overline{ab}\) \(\times\) 13 = 1001
\(\overline{ab}\) = 1001: 13
\(\overline{ab}\) = 77
Kết luận: Số thỏa mãn đề bài là 77

Gọi số phải tìm là abcde
Ta có phép nhân
abcde7
x 4
=7abcde
Lần lượt tìm các chữ số
7x4 có tận cùng là e =>e=8 nhớ 2
4e+2 có tận cùng bằng d =>d=4 nhớ 3
4d +3 có tận cùng bằng c =>c=9 nhớ 1
4c +1 có tận cùng bằng b =>b=7 nhớ 3
4b +3 có tận cùng bằng a =>a=1 nhớ 3
4a +3 có tận cùng bằng 7 (đúng với kết quả vừa tìm)
Vậy abcde=17948
thử lại 179487x4=717948

17: Gọi số cần tìm là X
Theo đề, ta có: 1000+10x+1=23X
=>13X=1001
=>X=77
16:
Gọi số cần tìm là X
Theo đề, ta có: \(10X+2=3\left(200000+X\right)\)
=>7X=600000-2=599998
=>X=85714

Gọi số cần tìm là abcde chữ số viết thêm là f ta có
abcdef = 3.fabcde => 10.abcde + f = 300000.f + 3.abcde => 7.abcde = 299999.f
=> abcde = 42857.f
=> \(f\ne0;f< 3\) vì nếu \(f\ge3\) thì 42857.f sẽ là số có 6 chữ số
+ Nếu f = 1 => abcde = 42857
Thử lại: 428571:142857 = 3
+ Nếu f=2 => abcde = 42857x2=85714
Thử lại: 857142:285714=3

2:
Gọi số cần tìm có dạng là \(\overline{X3}\)
Theo đề, ta có: \(\overline{X3}-\overline{X}=1992\)
=>10X+3-X=1992
=>9X=1989
=>X=221
Vậy: Số cần tìm là 2213

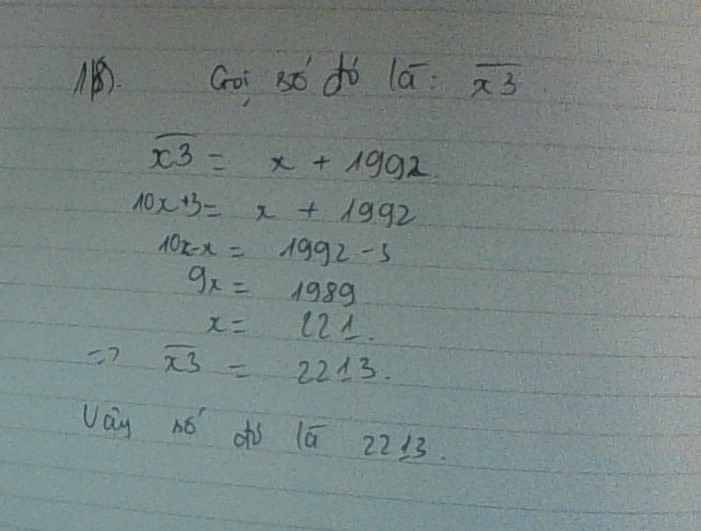
chỉ coi