Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc dự định đi hết quãng đường là x(km/h) và thời gian dự định là y (giờ0 với x;y>0
Độ dài quãng đường AB: \(xy\) (km)
Do người đó tăng vận tốc thêm 25km/h thì đến sớm hơn 1 giờ nên:
\(\left(x+25\right)\left(y-1\right)=xy\)
Do người đó giảm vận tốc 20km/h thì đến muộn hơn 2 giờ nên:
\(\left(x-20\right)\left(y+2\right)=xy\)
Ta có hệ: \(\left\{{}\begin{matrix}\left(x+25\right)\left(y-1\right)=xy\\\left(x-20\right)\left(y+2\right)=xy\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x+25y=25\\2x-20y=40\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=50\\y=3\end{matrix}\right.\)
Quãng đường: \(50.3=150\left(km\right)\)

Bắt Hết!!!
Lệch vận tốc là 20km/h
Lệch thời gian là 3 giờ
=> Quãng đường là: S=60km
vt=60
(v-10)(t+1)=60
(v+10)(t-1)=60
Giải ra dduocj v, t

Gọi vận tốc dự định và thời gian dự định là x và y (x,y>0). Theo đề bài ta có:
Nếu thời gian tăng thêm 14 km/h thì đến B sớm hơn 2 giờ nên ta có phương trình: \(\left(x+14\right)\left(y-2\right)=xy\Leftrightarrow xy-2x+14y-28=xy\Leftrightarrow-2x+14y=28\Leftrightarrow-x+7y=14\left(1\right)\)(do cả hai tích trên đều bằng độ dài quãng đường)
Nếu giảm vận tốc đi 4km/h thì đến B muộn 1 h nên ta có phương trình:
\(\left(x-4\right)\left(y+1\right)=xy\Leftrightarrow xy+x-4y-4=xy\Leftrightarrow x-4y=4\left(2\right)\) (do cả hai tích đều bằng độ dài quãng đường)
Từ (1) và (2) ta có hệ phương trình: \(\left\{{}\begin{matrix}-x+7y=14\left(1\right)\\x-4y=4\left(2\right)\end{matrix}\right.\)
Cộng từng vế của (1) và (2) ta được :
3y=18 ⇔ y=6 Thay vào (2) ta được: \(x-6\cdot4=4\Leftrightarrow x=4+24=28\)
Vậy vận tốc dự định và thời gian dự định là 28km/h và 6h

Gọi vận tốc dự định là x>4 (km/h) và thời gian dự định là y>2 (giờ)
Quãng đường \(S=xy\) (km)
Quãng đường nếu tăng vận tốc thêm 6km/h:
\(S=\left(x+6\right)\left(y-2\right)\)
Quãng đường nếu giảm vận tốc đi 4 km/h:
\(S=\left(x-4\right)\left(y+2\right)\)
Do độ dài quãng đường không đổi nên ta có hệ:
\(\left\{{}\begin{matrix}\left(x+6\right)\left(y-2\right)=xy\\\left(x-4\right)\left(y+2\right)=xy\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2x+6y=12\\2x-4y=8\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=24\\y=10\end{matrix}\right.\)

Gọi vận tốc của oto là x (km/h), x > 15 và thời gian đi từ A đến B của oto là y (h), y > 1
Vậy quãng đường AB là: xy (km)
Nếu vận tốc tăng thêm 30 km/h thì thời gian đi sẽ giảm 1 giờ. Vậy quãng đường AB là: (x + 30)(y - 1) (km)
Nếu vận tốc giảm bớt 15 km/h thì thời gian đi tăng thêm 1 giờ. Vậy quãng đường AB là: (x - 15)(y + 1)
Vậy ta có hệ phương trình:
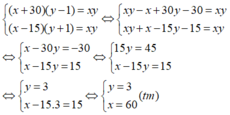
Vậy vận tốc của oto là 60 (km/h) và thời gian oto đi từ A đến B là 3 (h)

Gọi \(x\left(km/h\right)\) là vận tốc theo dự định \(\left(x>0\right)\)
\(y\left(h\right)\) là thời gian theo dự định \(\left(y>0\right)\)
Vì vận tốc tăng thêm \(14km/h\) thì đến sớm \(2h\) nên ta có phương trình:
\(xy=\left(x+14\right)\left(y-2\right)\\ \Leftrightarrow xy=xy-2x+14y-28\\ \Leftrightarrow-2x+14y=28 \left(1\right)\)
Vì vận tốc giảm đi \(4km/h\) thì đến muộn \(1h\) nên ta có phương trình:
\(xy=\left(x-4\right)\left(y+1\right)\\ \Leftrightarrow xy=xy+x-4y-4\\ \Leftrightarrow x-4y=4 \left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta có hệ phương trình: \(\left\{{}\begin{matrix}-2x+14y=28\\x-4y=4\end{matrix}\right.\)
Giải hệ phương trình ta được \(\left\{{}\begin{matrix}x=28\\y=6\end{matrix}\right.\)
Vậy vận tốc theo dự định là \(28km/h\)
thời gian theo dự định là \(6h\)
Cậu chép mạng nhé, mình tìm đc link rồi
Mình sẽ xóa câu trả lời của bạn

Gọi vận tốc dự định của ô tô là x (km/h) (x > 15)
Thời gian dự định đi của ô tô là y (h) (y > 1)
⇒ Quãng đường AB là xy (km)
Nếu vận tốc tăng 30 km/h thì thời gian giảm đi 1h nên ta có phương trình:
(x + 30)(y - 1) = xy ⇔ -x + 30y = 30 (1)
Nếu vận tốc giảm 15 km/h thì thời gian tăng 1h nên ta có phương trình
(x - 15)(y + 1) = xy ⇔ x - 15y = 15 (2)
Từ (1) và (2) ta có hệ phương trình:
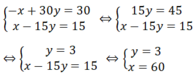
Vậy vận tốc đi từ A đến B là 60 km/h
Thời gian đi từ A đến B là 3h.