Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giải thích cặn kẽ như sau:
do xe máy và xe đạp di chuyển ngược nhau và gặp nhau tại một điểm nên ta có:
t1=t2(t1 là của xe máy,t2 là của xe đạp)
\(\Leftrightarrow\frac{S_1}{v_1}=\frac{S_2}{v_2}\)
\(\Leftrightarrow\frac{S_1}{30}=\frac{S_2}{10}\)
mà quãng đường xe máy cộng quãng đường xe đạp bằng quãng đường AB(S1+S2=S=60)(cái này vẽ sơ đồ là biết)
\(\Rightarrow S_2=60-S_1\)
thế vào phương trình trên ta có:
\(\frac{S_1}{30}=\frac{60-S_1}{10}\)
giải phương trình ta được S1=45km,S2=15km
từ đó ta có t1=1.5 giờ và điểm gặp cách A 45km
Gọi t là thời gian 2 xe gặp nhau:
Vì 2 xe đi ngược chiều nên
t= \(\frac{s}{v_1+v_2}=\frac{60}{30+10}=\frac{3}{2}=1,5\left(h\right)=1h30'\)
Vị trí gặp nhau đó cách A:
L=v1.t= 30.1,5=45(km)

ta có:
S1+S2=180
\(\Leftrightarrow v_1t_1+v_2t_2=180\)
\(\Leftrightarrow30t_1+15t_2=180\)
mà t1=t2=t
\(\Rightarrow45t=180\)
\(\Rightarrow t=4h\)
\(\Rightarrow S_1=120km\)
sau bao lâu 2 người gặp nhau là
SAB=S1+S2=V1.t1+V2.t2
Do t1=t2=t
\(\rightarrow\)SAB=(V1+V2).t
\(\rightarrow t=\dfrac{S_{AB}}{V_1+V_2}=\dfrac{180}{30+15}=4\left(h\right)\)
chỗ gặp nhau đó cách A là
S1=V1.t=30.4=120(km)
chỗ gặp nhau đó cách B là
S2=V2.t=15.4=60(km)

a) gọi t là thời gian 2 người đó gặp nhau
Vì họ xuất phát cùng 1 điểm và đi ngược chiều nhau nên ta có:
Ta có: t=\(\frac{s}{v_1+v_2}=\frac{150}{25+12.5}=4\left(h\right)\)
b) Chỗ gặp cách B là
L= t x v2= 4 x 12.5=50(km)
Vậy họ gặp nhau sau 4 h cách B 12.5 km

Thời điểm xe gặp nhau là:
Ta có: \(s_1+s_2=s_{AB}\Leftrightarrow v_1\left(6+t\right)+v_2.\left(7+t\right)=114\Leftrightarrow t\left(v_1+v_2\right)=114+6v_1+7v_2\)
\(\Leftrightarrow t=\dfrac{114+6v_1+7v_2}{v_1+v_2}=9\left(h\right)\)
Nơi gặp cách A: \(s_1=\left(t-6\right).v_1=\left(9-6\right).18=54\left(km\right)\)

Thời gian người đi xe đạp đi trước người đi bộ là 2h nhưng người đi xe đạp lại nghỉ 1h nên ta coi người đi xe đạp đi trước người đi bộ 1h.
Sau 1h thì người đi xe đạp đi được: \(S_1 = 12 . 1 = 12 (km)\)
Vậy ta có thể coi 2 người bắt đầu đi từ lúc 8h, và khoảng cách giữa 2 người là \(\Delta S = AB - S_1 = 36 km\)
Kể từ lúc 8h thì thời gian để 2 người gặp nhau là:\( \Delta t = \frac{\Delta S}{12 + 4} = 2,25 (h)\)
Vậy 2 người gặp nhau lúc 10h15phút; và cách A là: \(S = S_1 + 12 . 2,25 = 39 km\)

Chọn mốc thời gian tại 6h.
Chọn mốc quãng đường tại A.
Phương trình cho hai xe lần lượt là:
+Xe 1: s1=v1
+Xe 2: s2= v2t1 - v2ttrễ
Khi 2 xe gặp nhau ta có:
s1=s2
\(\Leftrightarrow\)v1t1= v2t1 - v2ttrễ
\(\Leftrightarrow\)v2ttrễ = v2t1 - v1t1 (Chuyển vế đổi dấu)
\(\Leftrightarrow\)v2ttrễ = t1(v2-v1) (Đặt nhân tử chung)
\(\Leftrightarrow\)t1=\(\dfrac{v_2t_{trễ}}{v_2-v_1}\) (Phương trình tìm x bình thường)
\(\Leftrightarrow\)t1=\(\dfrac{30}{30-18}\) (Vì ttrễ=1h nên mình hk thế số)
\(\Leftrightarrow\)t1=2,5 (h)
Vậy sau 2h30' nữa 2 xe gặp nhau
Vị trí gặp cách A là:
s1=v1t1
\(\Leftrightarrow\)s1=18*2,5=45km
tương tự ta có s2=sAB-s1=114-45=69km
Xong!

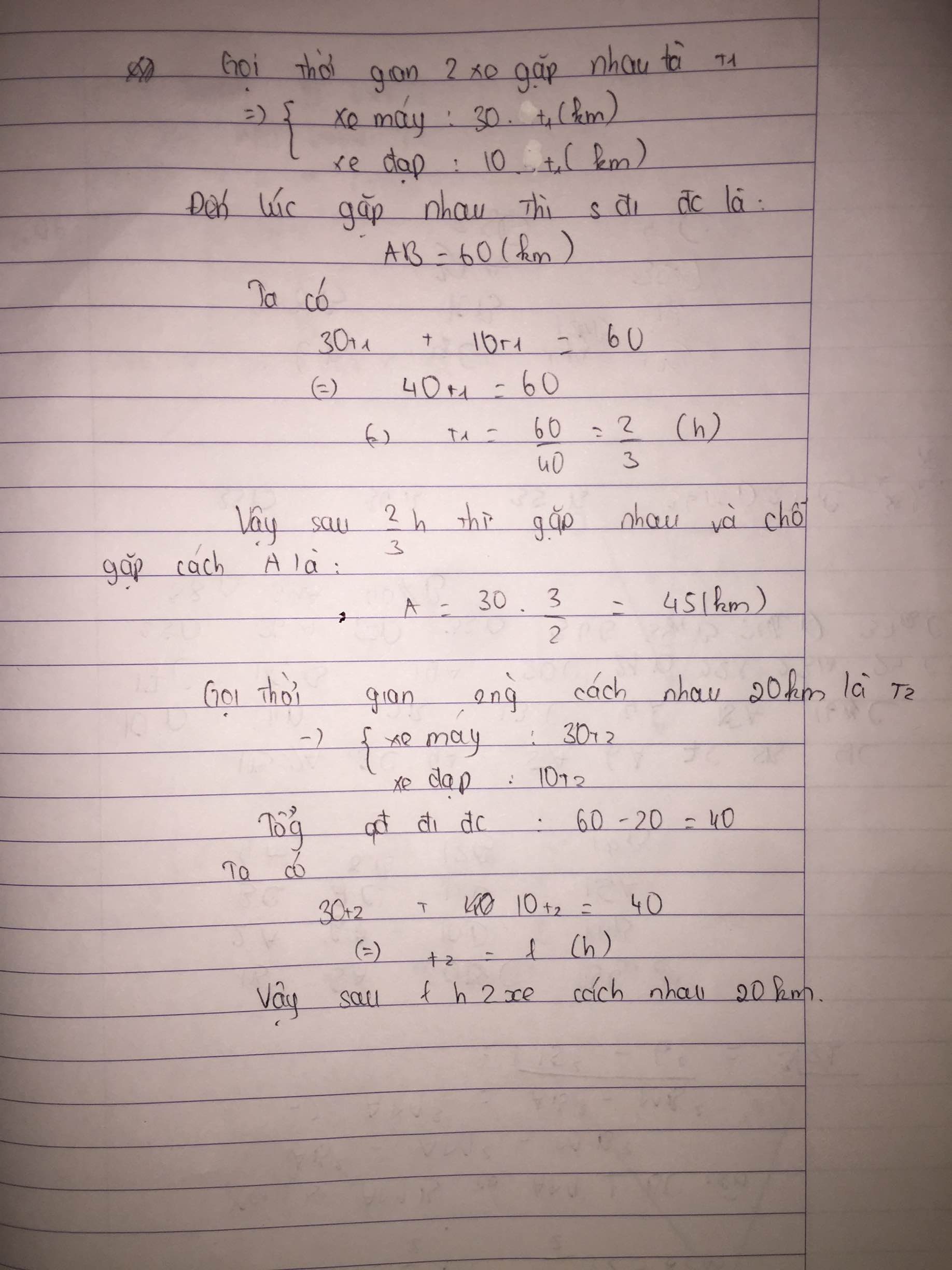
a, Gọi t là t/g 2 xe gặp nhau
Vì 2 xe ngược chiều nên \(t=\dfrac{s}{v_1+v_2}=\dfrac{40}{30+10}=1\left(h\right)\)
Vậy sau 1 giờ thì 2 xe gặp nhau
Chỗ gặp nhau cách A \(v_1\cdot t=1\cdot30=30\left(km\right)\)
b, Để 2 ng cách nhau 10km thì \(s_1+10=AB+s_2\)
\(\Leftrightarrow30t+10=40+10t\\ \Leftrightarrow t=\dfrac{30}{20}=1,5\left(h\right)\)
Vậy sau 1,5 giờ thì 2 ng cách nhau 10km