Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi thời gian dự định là $a$ (giờ)
Theo bài ra ta có:
$AB=10a=10.1+(10+10)(a-1-1)$
$\Leftrightarrow 10a=10+20(a-2)$
$\Leftrightarrow a=3$ (giờ)
Độ dài quãng đường $AB$ là: $10a=10.3=30$ (km)

Bài giải
Gọi quãng đường AB là x (km) (x \(\inℕ^∗\))
=> Thời gian để ô tô đi từ A đến B với vận tốc 40 km/h và không gặp chướng ngại vật nào là: x : 40
Theo đề bài: 40.1 + 48.(x : 40 - 1,5) = x
=> 40 + 48.x : 40 - 48.1,5 = x
=> 40 + 1,2.x - 72 = x
=> 72 - 40 = 1,2.x - x
=> 32 = 0,2.x
=> x = 32 : 0,2
=> x = 160 (km)
Vậy quãng đường AB dài 160 km

Bài 1:
Gọi x(km) là độ dài quãng đường AB(Điều kiện: x>0)
Thời gian dự định của ô tô để đi hết quãng đường AB là: \(\dfrac{x}{50}\left(h\right)\)
Thời gian thực tế của ô tô để đi hết quãng đường AB là:
\(2+\dfrac{1}{4}+\dfrac{x-112.5}{55}=\dfrac{x-112.5}{55}+\dfrac{9}{4}\)
Do đó, ta có phương trình:
\(\dfrac{x-112.5}{55}+\dfrac{9}{4}=\dfrac{x}{50}\)
\(\Leftrightarrow\dfrac{20\left(x-112.5\right)}{1100}+\dfrac{2475}{1100}=\dfrac{22x}{1100}\)
\(\Leftrightarrow20x-2250+2475-22x=0\)
\(\Leftrightarrow-2x+225=0\)
\(\Leftrightarrow x=\dfrac{225}{2}\left(nhận\right)\)
Vậy: \(AB=\dfrac{225}{2}km\)

gọi quãng đường AB là: x (km;x>0)
=> thời gian dđ đi hết S: x/20
quãng đường đi được trong nửa h khởi hành: 1/2 .20=10 km
=> S còn lại: x-10
thời gian đi S còn lại: x-10/24
đổi 15'=1/4 h
vì vẫn đến kịp nên ta có pt: \(\frac{1}{2}+\frac{1}{4}+\frac{x-10}{24}=\frac{x}{20}\Leftrightarrow\frac{24x-20x+200}{480}=\frac{3}{4}\Leftrightarrow4x+800=1440\Leftrightarrow x=160\)(t/m đk)
=> S AB là: 160km. thời gian đi hết S: 160:20=8h
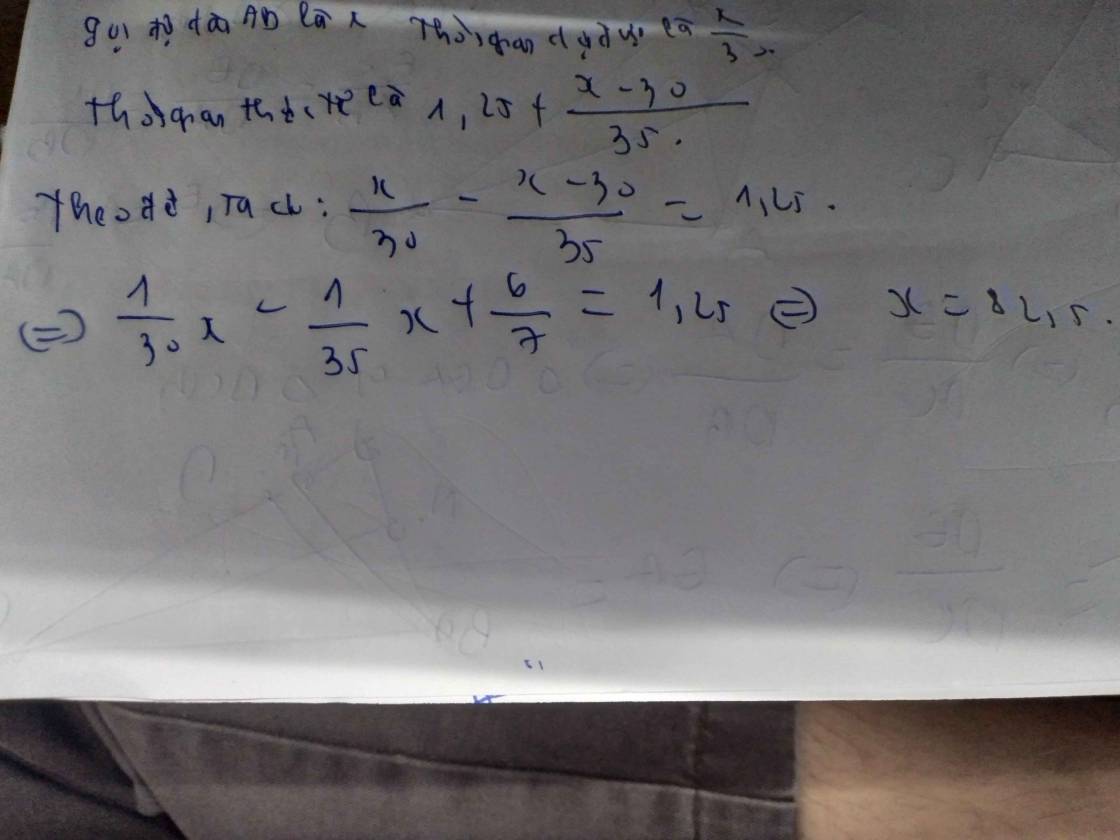
gọi x là vận tốc ban đầu của người đó(km/h) (x>0)
vận tốc sau khi tăng là x+4 (km/h)
thời gian đi hết quãng đường theo dự định là 60/x(h)
sau 1h xe đi dược quãng đường là 1*x(km) nên quãng đường còn lại là 60-x(km)
thời gian đi hết quãng đường theo thực tế là : \(1+\dfrac{20}{60}+\dfrac{60-x}{x+4}=1+\dfrac{1}{3}+\dfrac{60-x}{x+4}\) (h)
vì xe đến đúng thời gian đã định nên ta có phương trình:
\(\dfrac{60}{x}=1+\dfrac{1}{3}+\dfrac{60-x}{x+4}\\ \Leftrightarrow\dfrac{60}{x}=\dfrac{3\left(x+4\right)+x+4+3\left(60-x\right)}{3\left(x+4\right)}\\ \Leftrightarrow\dfrac{60\cdot3\left(x+4\right)}{x\cdot3\left(x+4\right)}=\dfrac{x\left(3x+12+x+4+180-3x\right)}{3x\left(x+4\right)}\\ \Leftrightarrow180x+720=x\left(x+196\right)\Leftrightarrow180x+720=x^2+196x\\ \Leftrightarrow-x^2+180x-196x+720=0\\ \Leftrightarrow-\left(x^2+16x-720\right)=0\\ \Leftrightarrow-\left(x-20\right)\left(x+36\right)=0\Leftrightarrow\left[{}\begin{matrix}x=20\left(TM\right)\\x=-36\left(loại\right)\end{matrix}\right.\)
vậy vận tốc ban đầu của người đó là 20(km/h)