Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ hình vẽ suy ra để F song song với BC
\(\Rightarrow \tan\widehat{B}=\dfrac{F_b}{F_c}=\dfrac{AC}{AB}\)
Từ đó bạn có thể tính giá trị \(q_a\)
Lưu ý dấu giá trị tuyệt đối nên sẽ có hai giá trị của qA tương đương với trường hợp F như hình trên nhưng nó có chiều quay ngược lại.

a, Lực điện tương tác giữa hai điện tích là
Fđ = \(9.10^9.\dfrac{\left|-10^{-7}.5.10^{-8}\right|}{0.05^2}=0.018\left(N\right)\)
b, Ta có AC2 + BC2 = AB2 (32 + 42 = 52) nên theo định lí đảo của định lí Pitago ta có tam giác vuông ABC tại C
Lực điện tổng hợp bằng 1 nửa lực điện ở câu A (vẽ hình là thấy)
độ lớn bằng 0.009 N
c, Mình chưa học, nhưng chắc chỉ cần dùng ct là xong

a, ta thấy AM+BM=AB
\(F_1=k.\dfrac{\left|q_1q_0\right|}{AM^2}=3,75\left(N\right)\)
\(F_2=k\dfrac{\left|q_2q_0\right|}{BM^2}=5,625\left(N\right)\)
\(\Rightarrow F=\left|F_1-F_2\right|=1,875\left(N\right)\)
b, để ý thấy \(AB^2=AN^2+BN^2\)
\(\Rightarrow F_1\perp F_2\)
\(F_1=k.\dfrac{\left|q_1q_0\right|}{AN^2}=3,75\left(N\right)\)
\(F_2=k.\dfrac{\left|q_2q_0\right|}{BN^2}=1,40625\left(N\right)\)
\(\Rightarrow F=\sqrt{F_1^2+F_2^2}\approx4\left(N\right)\)
c, ta thấy AI=BI=AB=1m
vecto lực tương tác là tam giác đêu \(\alpha=60^o\)
\(F_1=k\dfrac{\left|q_1q_0\right|}{AI^2}=1,35\left(N\right)\)
\(F_2=k.\dfrac{\left|q_2q_0\right|}{BI^2}=0,9\left(N\right)\)
\(\Rightarrow F=\sqrt{F_1^2+F_2^2+2F_1F_2cos\alpha}=...\)


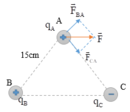
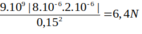
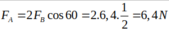
1)lực tĩnh điện đẩy nhau cảu A và B là :
9*10^(9)*((1.8*10^(-8)*5.4*10^(-9))/0.03^(2))=9.72*10^(-4) N
gọi X là q c
vì tổng lục tĩnh điện tác dụng lên A ss with BC nên
ta có pt
9.72*10^(-4)+(9*10^(9)*((1.8*10^(-8)*X)/0.04^(2))=9*10^(9)*((5.4*10^(-9)*X)/0.056(2))
giải tìm được X=-1.8*10^(-8)
không chắc đúng đâu !
hình như sai cái gì đó chổ pt thay 0.05^(2) =>0.5^(2)
ta được X=-9.6*10^(-9)