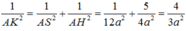Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(OC=\dfrac{1}{2}AC\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}d\left(A;\left(SCD\right)\right)\)
Kẻ \(AH\perp SD\Rightarrow AH\perp\left(SCD\right)\)
\(\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\sqrt{2}\)
\(\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}AH=\dfrac{\sqrt{2}}{2}\)


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
E=AB∩CD,G=EN∩SB⇒GE=AB∩CD,G=EN∩SB⇒G là trọng tâm tam giác SAE.
d(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14hd(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14h
Tứ diện AEND vuông tại đỉnh A nên 1h2=1AN2+1AE2+1AD2=116a2⇒h=a√66111h2=1AN2+1AE2+1AD2=116a2⇒h=a6611
Vậy d(M,(NCD))=a√6644.d(M,(NCD))=a6644.

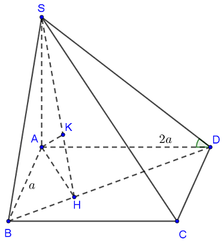
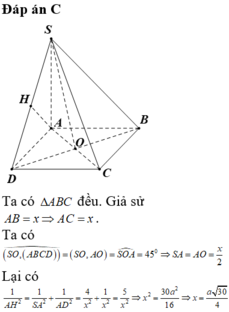
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow SA=AB.tan45^0=a\)
Gọi O là tâm đáy \(\Rightarrow AO=CO\Rightarrow d\left(C;\left(SBD\right)\right)=d\left(A;\left(SBD\right)\right)\)
Kẻ AH vuông góc BD, kẻ AK vuông góc SH
\(\Rightarrow AK\perp\left(SBD\right)\Rightarrow AK=d\left(A;\left(SBD\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{1}{a^2}+\dfrac{1}{4a^2}=\dfrac{5}{4a^2}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{SA^2}+\dfrac{1}{AK^2}=\dfrac{1}{a^2}+\dfrac{5}{4a^2}=\dfrac{9}{4a^2}\)
\(\Rightarrow AK=\dfrac{2a}{3}\Rightarrow d\left(C;\left(SBD\right)\right)=\dfrac{2a}{3}\)

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được

d(B;(SCD))=1/2*d(A;(SCD))
Gọi giao của AB và CD là E
BC//AD
=>EB/EA=EC/ED=BC/AD=1/2
=>ΔAED cân tại E
=>AC vuông góc DE
Kẻ AF vuông góc SC
\(AC=\sqrt{2^2-1^2}=\sqrt{3}\left(cm\right)\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{6}\left(cm\right)\)
=>\(AF=d\left(A;\left(SCD\right)\right)=\dfrac{3}{\sqrt{6}}=\dfrac{\sqrt{6}}{2}\left(cm\right)\)
=>\(d\left(B;\left(SCD\right)\right)=\dfrac{\sqrt{6}}{4}\left(cm\right)\)

S A B C D H E K F
Ta có
\(SH\perp\left(ABCD\right);SH\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(ABCD\right)\)
Trong mp (ABCD) từ C dựng đường thẳng vuông góc với BD cắt BD tại F ta có
\(SH\perp\left(ABCD\right);CF\in ABCD\Rightarrow SH\perp CF\)
Mà \(CF\perp BD\)
Ta có \(BD\in\left(SBD\right);SH\in\left(SBD\right)\)
\(\Rightarrow CF\perp\left(SBD\right)\) => CF là khoảng cách từ C đến (SBD)
Trong mp (ABCD) nối CH cắt AD tại E
Ta có BC//AD \(\Rightarrow\dfrac{BC}{ED}=\dfrac{HB}{HD}=\dfrac{HC}{HE}=1\Rightarrow ED=BC=\dfrac{3a}{2}\)
\(\Rightarrow EA=AD-ED=3a-\dfrac{3a}{2}=\dfrac{3a}{2}=BC\)
Mà BC//AE và \(\widehat{ABC}=90^o\)
=> ABCE là hình chữ nhật
Trong mp (ABCD) từ H dựng đường thẳng vuông góc với CD cắt CD tại K
Xét tg vuông CDE có
\(CD=\sqrt{CE^2+ED^2}=\sqrt{4a^2+\dfrac{9a^2}{4}}=\dfrac{5a}{2}\)
Xét tg vuông ABD có
\(BD=\sqrt{AB^2+AD^2}=\sqrt{4a^2+9a^2}=a\sqrt{13}\)
\(\Rightarrow HB=HD=\dfrac{BD}{2}=\dfrac{a\sqrt{13}}{2}\)
Xét tg vuông CKH và tg vuông CED có \(\widehat{ECD}\) chung
=> tg CKH đồng dạng với tg CED (g.g.g)
\(\Rightarrow\dfrac{CK}{CE}=\dfrac{HC}{CD}\Rightarrow CK=\dfrac{CE.HC}{CD}=\dfrac{2a.a}{\dfrac{5a}{2}}=\dfrac{4a}{5}\)
Xét tg vuông CKH có
\(HK=\sqrt{HC^2-CK^2}=\sqrt{a^2-\dfrac{16a^2}{25}}=\dfrac{3a}{5}\)
Xét tg vuông DKH và tg vuông DFC có \(\widehat{BDC}\) chung
=> tg DKH đồng dạng với tg DFC (g.g.g)
\(\Rightarrow\dfrac{HK}{CF}=\dfrac{HD}{CD}\Rightarrow CF=\dfrac{HK.CD}{HD}=\dfrac{\dfrac{3a}{5}.\dfrac{5a}{2}}{\dfrac{a\sqrt{13}}{2}}=\dfrac{3a\sqrt{13}}{13}\)

a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ