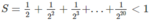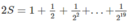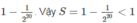DT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
1
AK
25 tháng 2 2018
1 - 1/2 + 1/3 - 1/4 + .. + 1/121 - 1/122 + 1/123
= ( 1 + 1/3 + ... + 1/121 + 1/123 ) - ( 1/2 + 1/4 + .. + 1/122 )
Đến bước này ta sẽ cùng cộng 2 vế với : 1/2 + 1/4 + .. + 1/122
= ( 1 + 1/2 + 1/3 + 1/4 + ...+ 1/121 + 1/122 + 1/123 ) - 2. ( 1/2 + 1/4 + .. + 1/122 )
= ( 1 + 1/2 + 1/3 + ...+ 1/122 +1 /123 ) - ( 1 + 1/2 + ...+ 1/61 )
= 1/62 + 1/63 + ..+1/122 + 1/123
Chúc học giỏi !!
DT
0
28 tháng 2 2018
Xét \(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{123}\)
\(=\left(1+\frac{1}{3}+...+\frac{1}{121}+\frac{1}{123}\right)-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...+\frac{1}{122}\right)\)
\(=\left(1+\frac{1}{3}+...+\frac{1}{121}+\frac{1}{123}\right)-2\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{61}\right)\)
\(=\frac{1}{62}+\frac{1}{63}+\frac{1}{64}+...+\frac{1}{123}\)
NN
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 8 2023
A = \(\dfrac{3^{123}+1}{3^{125}+1}\) Vì 3123 + 1 < 2125 + 1 Nên A = \(\dfrac{3^{123}+1}{3^{125}+1}\)< \(\dfrac{3^{123}+1+2}{3^{125}+1+2}\)
A < \(\dfrac{3^{123}+3}{3^{125}+3}\) = \(\dfrac{3.\left(3^{122}+1\right)}{3.\left(3^{124}+1\right)}\) = \(\dfrac{3^{122}+1}{3^{124}+1}\) = B
Vậy A < B
CM
16 tháng 9 2019
Đáp án cần chọn là: D
M = 1 + 1 2 + 1 2 2 + 1 2 3 + ... + 1 2 99 + 2 2 100 2 M = 2. 1 + 1 2 + 1 2 2 + 1 2 3 + ... + 1 2 99 + 2 2 100 = 2 + 1 + 1 2 + 1 2 2 + 1 2 3 + ... + 1 2 99
Ta có :
M = 2 M − M = ( 2 + 1 + 1 2 + 1 2 2 + 1 2 3 + ... + 1 2 99 ) − ( 1 + 1 2 + 1 2 2 + 1 2 3 + ... + 1 2 99 + 2 2 100 ) M = 2 M − M = 2 + 1 + 1 2 + 1 2 2 + 1 2 3 + ... + 1 2 98 + 1 2 99 − 1 + 1 2 + 1 2 2 + 1 2 3 + ... + 1 2 99 + 1 2 100 = 2 − 1 2 100 = 2 101 − 1 2 100
PT
1
12 tháng 8 2023
a)\(...A=\dfrac{2^{50+1}-1}{2-1}=2^{51}-1\)
b) \(...\Rightarrow B=\dfrac{3^{80+1}-1}{3-1}=\dfrac{3^{81}-1}{2}\)
c) \(...\Rightarrow C+1=1+4+4^2+4^3+...+4^{49}\)
\(\Rightarrow C+1=\dfrac{4^{49+1}-1}{4-1}=\dfrac{4^{50}-1}{3}\)
\(\Rightarrow C=\dfrac{4^{50}-1}{3}-1=\dfrac{4^{50}-4}{3}=\dfrac{4\left(4^{49}-1\right)}{3}\)
Tương tự câu d,e,f bạn tự làm nhé