tính các góc của hình thang ABCD ( AB, CD là 2 đáy) biết \(\widehat{A}\) = \(2\widehat{D}\), \(\widehat{B}=\widehat{C}+40^o\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


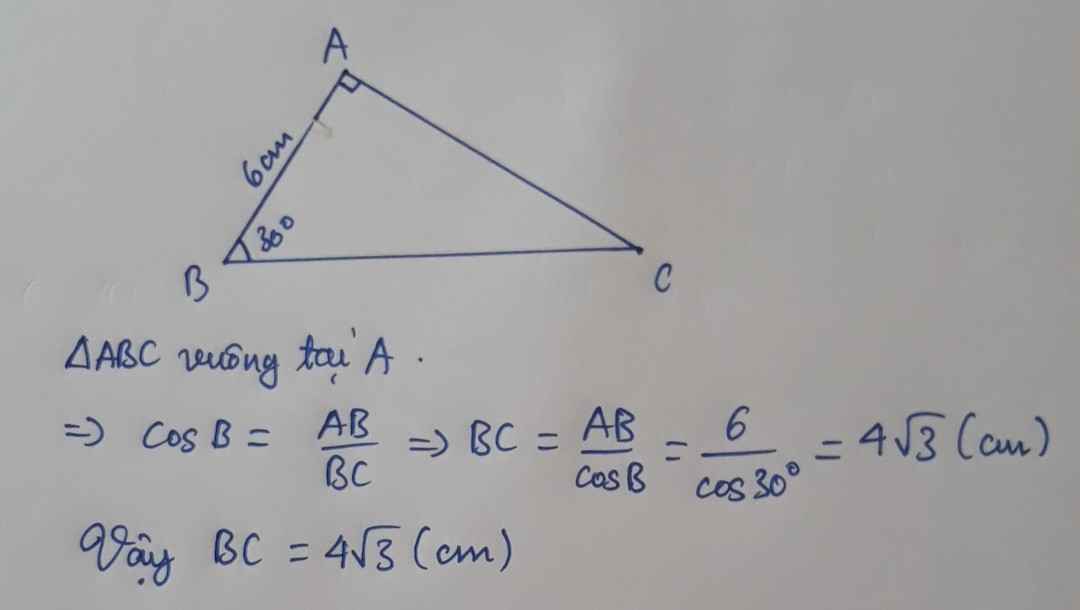
xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}\)
=>\(\dfrac{6}{BC}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(BC=6\cdot\dfrac{2}{\sqrt{3}}=4\sqrt{3}\left(cm\right)\)

\(\left|A+B\right|< =\left|A\right|+\left|B\right|\)
=>\(\left(\left|A+B\right|\right)^2< =\left(\left|A\right|+\left|B\right|\right)^2\)
=>\(A^2+B^2+2AB< =A^2+B^2+2\left|AB\right|\)
=>2AB<=2|AB|
=>AB<=|AB|(luôn đúng)
Dấu '=' xảy ra khi AB>=0

\(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{10\cdot11}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{10}-\dfrac{1}{11}\)
\(=1-\dfrac{1}{11}=\dfrac{10}{11}\)
\(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{10\cdot11}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}\\ =1-\dfrac{1}{11}\\ =\dfrac{11}{11}-\dfrac{1}{11}=\dfrac{10}{11}\)

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(\dfrac{6}{BC}=sin30=\dfrac{1}{2}\)
=>\(BC=6\cdot2=12\left(cm\right)\)

Ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\)(hai góc kề bù)
=>\(\widehat{yOz}+125^0=180^0\)
=>\(\widehat{yOz}=55^0\)
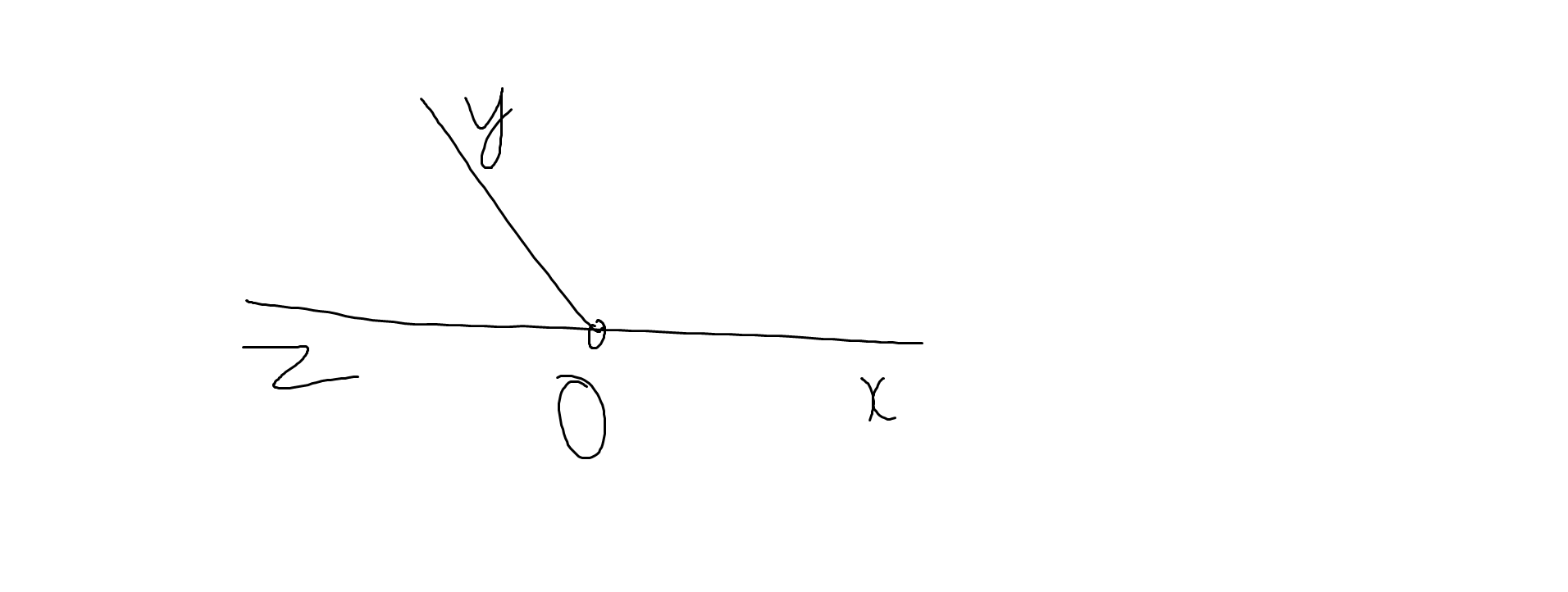

\(a+\dfrac{2}{b}=b+\dfrac{2}{c}\Rightarrow a-b=\dfrac{2}{c}-\dfrac{2}{b}=2\left(\dfrac{b-c}{bc}\right)\)
\(\Rightarrow\dfrac{a-b}{b-c}=\dfrac{2}{bc}\)
Tương tự: \(a+\dfrac{2}{b}=c+\dfrac{2}{a}\Rightarrow\dfrac{a-c}{b-a}=\dfrac{2}{ab}\)
\(b+\dfrac{2}{c}=c+\dfrac{2}{a}\Rightarrow\dfrac{b-c}{c-a}=\dfrac{2}{ca}\)
Nhân vế với vế:
\(\left(\dfrac{a-b}{b-c}\right)\left(\dfrac{a-c}{b-a}\right)\left(\dfrac{b-c}{c-a}\right)=\dfrac{8}{\left(abc\right)^2}\)
\(\Rightarrow\left(abc\right)^2=8\)
\(\Rightarrow\left|abc\right|=2\sqrt{2}\)

\(\dfrac{2}{3}\times\dfrac{3}{5}+\dfrac{1}{3}:\dfrac{3}{4}\)
\(=\dfrac{2}{5}+\dfrac{1}{3}\times\dfrac{4}{3}\)
\(=\dfrac{2}{5}+\dfrac{4}{9}=\dfrac{18}{45}+\dfrac{20}{45}=\dfrac{38}{45}\)
\(\dfrac{2}{3}\) x \(\dfrac{3}{5}\) + \(\dfrac{1}{3}\) : \(\dfrac{3}{4}\)
= \(\dfrac{2}{5}\) + \(\dfrac{1}{3}\) x \(\dfrac{4}{3}\)
= \(\dfrac{2}{5}\) + \(\dfrac{4}{9}\)
= \(\dfrac{18}{45}\) + \(\dfrac{20}{45}\)
= \(\dfrac{38}{45}\)

Min P em có thể tự tìm đơn giản bằng AM-GM
Min R cũng khá đơn giản:
Đặt \(\left(\sqrt[3]{a};\sqrt[3]{b};\sqrt[3]{c}\right)=\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}0\le x;y;z\le1\\x^3+y^3+z^3=\dfrac{9}{8}\end{matrix}\right.\)
\(R=\dfrac{1}{1+x}+\dfrac{1}{1+y}+\dfrac{1}{1+z}\ge\dfrac{9}{3+x+y+z}\ge\dfrac{9}{3+\sqrt[3]{9\left(x^3+y^3+z^3\right)}}=\dfrac{6}{2+\sqrt[3]{3}}\)
Xét \(Q=x+y+z\)
Do \(\left(x+y+z\right)^3\ge x^3+y^3+z^3=\dfrac{9}{8}\Rightarrow x+y+z\ge\sqrt[3]{\dfrac{9}{8}}>1\Rightarrow Q-1>0\)
\(x^3+y^3+z^3=\left(x+y+z\right)^3-3\left(x+y+z\right)\left(xy+yz+zx\right)+3xyz\)
\(\Rightarrow\dfrac{9}{8}=Q^3-3Q\left(xy+yz+zx\right)+3xyz\)
\(\Rightarrow\dfrac{9}{8}=Q^3-3\left(Q-1\right)\left(xy+yz+zx\right)-3\left(xy+yz+zx-xyz\right)\)
Do \(0\le x;y;z\le1\Rightarrow\left(1-x\right)\left(1-y\right)\left(1-z\right)\ge0\)
\(\Rightarrow xy+yz+zx-xyz\ge Q-1\) (1)
\(\Rightarrow xy+yz+zx\ge xyz+Q-1\ge Q-1\) (2)
(1);(2)\(\Rightarrow\dfrac{9}{8}\le Q^3-3\left(Q-1\right)\left(Q-1\right)-3\left(Q-1\right)\)
\(\Rightarrow8Q^3-24Q^2+24Q-9\ge0\)
\(\Rightarrow\left(2Q-3\right)\left(4Q^2-6Q+3\right)\ge0\)
Do \(4Q^2-6Q+3=4\left(Q-\dfrac{3}{4}\right)^2+\dfrac{3}{4}>0;\forall Q\)
\(\Rightarrow2Q-3\ge0\Rightarrow Q\ge\dfrac{3}{2}\)
\(Q_{min}=\dfrac{3}{2}\) khi \(\left(x;y;z\right)=\left(0;1;\dfrac{1}{2}\right)\) và hoán vị hay \(\left(a;b;c\right)=\left(0;1;\dfrac{1}{8}\right)\) và hoán vị

- Nếu n là số lẻ :
\(2024^n=4^n.506^n=\overline{...6}.\overline{...6}=\overline{...6}\)
\(\Rightarrow2024^n-1=\overline{.....5}⋮10^{2023}=\overline{...0}\)
- Nếu n là số chẵn :
\(2024^n=4^n.506^n=\overline{...1}.\overline{...6}=\overline{...6}\)
\(\Rightarrow2024^n-1=\overline{.....5}⋮10^{2023}=\overline{...0}\)
Vậy suy ra \(đpcm\)
AB//CD
=>\(\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{C}+\widehat{C}+40^0=180^0\)
=>\(2\cdot\widehat{C}=180^0-40^0=140^0\)
=>\(\widehat{C}=70^0\)
\(\widehat{B}=70^0+40^0=110^0\)
ABCD là hình thang có AB//CD
=>\(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)
=>\(2\cdot\widehat{D}+\widehat{D}=180^0\)
=>\(3\widehat{D}=180^0\)
=>\(\widehat{D}=60^0\)
\(\widehat{A}=2\cdot60^0=120^0\)