Lời giải:

Áp dụng định lý Viet:

$x_1+x_2=5$
$x_1x_2=1$

Khi đó:

\(M=\frac{|x_1-x_2|}{\sqrt{x_1}+\sqrt{x_2}}\Rightarrow M^2=\frac{|x_1-x_2|^2}{(\sqrt{x_1}+\sqrt{x_2})^2}=\frac{x_1^2+x_2^2-2x_1x_2}{x_1+x_2+2\sqrt{x_1x_2}}\\ =\frac{(x_1+x_2)^2-4x_1x_2}{x_1+x_2+2\sqrt{x_1x_2}}=\frac{5^2-4.1}{5+2\sqrt{1}}=3\)

Lời giải:

Lấy PT(1)*2 -PT(2) thu được:

$2(x+2y)-(2x-3y)=2(m+3)-m$

$\Leftrightarrow 7y=m+6$

$\Leftrightarrow y=\frac{m+6}{7}$

$x=m+3-2y=m+3-\frac{2(m+6)}{7}=\frac{5m+9}{7}$

Vậy HPT luôn có nghiệm $(x,y)=(\frac{5m+9}{7}, \frac{m+6}{7})$
Để $x+y=-3$
$\Leftrightarrow \frac{5m+9}{7}+\frac{m+6}{7}=-3$

$\Leftrightarrow \frac{6m+15}{7}=-3$

$\Rightarrow 6m+15=-21$

$\Rightarrow m = -6$ 

pt thứ hai \(\Leftrightarrow\) \(y^2-\left(3x+2\right)y+2x^2+3x+1=0\) (*)

Ta có \(\Delta=\left[-\left(3x+2\right)\right]^2-4\left(2x^2+3x+1\right)\)

\(=9x^2+12x+4-8x^2-12x-4\)

\(=x^2\ge0\) 

Do đó (*) có 2 nghiệm là \(\left[{}\begin{matrix}y=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3x+2+\sqrt{x^2}}{2}=\dfrac{3x+2+\left|x\right|}{2}\\y=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3x+2-\sqrt{x^2}}{2}=\dfrac{3x+2-\left|x\right|}{2}\end{matrix}\right.\)

Không mất tính tổng quát, giả sử \(x\ge0\). Khi đó:

\(\left[{}\begin{matrix}y=\dfrac{3x+2+x}{2}=\dfrac{4x+2}{2}=2x+1\\y=\dfrac{3x+2-x}{2}=\dfrac{2x+2}{2}=x+1\end{matrix}\right.\)

Nếu \(y=2x+1\) thì thay vào pt đầu tiên, ta có:

\(x^2+\left(2x+1\right)^2+x+2x+1=8\)

\(\Leftrightarrow5x^2+7x-6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\) \(\Rightarrow y=2x+1=2.\dfrac{3}{5}+1=\dfrac{11}{5}\)

Nếu \(y=x+1\) thì thế vào pt đầu tiên, ta có:

\(x^2+\left(x+1\right)^2+x+x+1=8\)

\(\Leftrightarrow2x^2+4x-6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-3\left(loại\right)\end{matrix}\right.\) \(\Rightarrow y=x+1=1+1=2\)

 Vậy ta tìm được 2 cặp nghiệm là \(\left(\dfrac{3}{5},\dfrac{11}{5}\right)\) và \(\left(1,2\right)\)

 Tương tự như vậy, xét TH \(x< 0\) thì ta tìm được thêm 2 cặp nghiệm chính là \(\left(-2,-3\right)\) và \(\left(-3,-2\right)\)

phương trình thứ 2 dấu = ở đâu vậy ạ

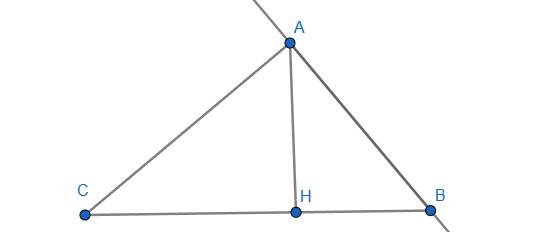
Xét tam giác ABC vuông tại A có AH là đường cao

\(BH.BC=AB^2\)

\(\Rightarrow\left(BC-HC\right)\cdot BC=AB^2\)

\(\Rightarrow\left(BC-19,2\right)\cdot BC=AB^2\)

\(\Rightarrow BC^2-19,2BC=12^2\)

\(\Rightarrow BC^2-19,2BC-144=0\)

\(\Rightarrow BC=\dfrac{48+12\sqrt{41}}{5}\approx24,96\left(cm\right)\)Xét tam giác ABC vuông tại A có

\(BC^2=AB^2+AC^2\)

\(\Rightarrow24,96^2=12^2+AC^2\)

\(\Rightarrow AC\approx21,89\left(cm\right)\)

Xét tam giác ABC vuông tại A có

\(S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}BC.AH\)

\(\Rightarrow\dfrac{1}{2}\cdot12\cdot21,89=\dfrac{1}{2}\cdot24,96\cdot AH\)

\(\Rightarrow AH=\dfrac{262,68}{24,96}\approx10,52\left(cm\right)\)

Vậy độ dài của $AC$ và $AH$ là: $AC\approx 21,89\text{cm và}$ $AH\approx 10,52\text{cm}$

Xét ΔABC vuông tại A có AH là đường cao

nên \(AB^2=BH\cdot BC\)

=>\(BH\left(BH+19,2\right)=12^2=144\)

=>\(BH^2+19,2\cdot BH-144=0\)

=>\(\left[{}\begin{matrix}BH=\dfrac{-19,2-\dfrac{24\sqrt{41}}{5}}{2}\left(loại\right)\\BH=\dfrac{-19,2+\dfrac{24\sqrt{41}}{5}}{2}=-9,6+\dfrac{12\sqrt{41}}{5}\left(nhận\right)\end{matrix}\right.\)

=>\(BH=\dfrac{-48+12\sqrt{41}}{5}\)

=>\(BC=\dfrac{-48+12\sqrt{41}}{5}+19,2=\dfrac{48+12\sqrt{41}}{5}\left(cm\right)\)

ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC=\dfrac{-48+12\sqrt{41}}{5}\cdot19,2=3,84\left(-48+12\sqrt{41}\right)\)

=>\(AH=\sqrt{3,84\left(-48+12\sqrt{41}\right)}\left(cm\right)\)

=>\(AC=\sqrt{AH^2+HC^2}=\sqrt{3,84\left(-48+12\sqrt{41}\right)+19,2^2}\)

=>\(AC=\sqrt{184,32+46,08\sqrt{41}}\)(cm)

\(\sqrt{x}+\sqrt{2-x}+\sqrt{2x-x^2}=3\) (ĐKXĐ: \(0\le x\le2\))

\(\Leftrightarrow\sqrt{x}+\sqrt{2-x}+\sqrt{x\left(2-x\right)}=3\) (1)

Đặt \(\sqrt{x}+\sqrt{2-x}=a\Rightarrow\dfrac{a^2-2}{2}=\sqrt{x\left(2-x\right)}\) (2) (a > 0)

Thay (2) vào (1), ta được:

\(a+\dfrac{a^2-2}{2}=3\)

\(\Leftrightarrow a^2+2a-2=6\)

\(\Leftrightarrow a^2+2a-8=0\) \(\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-4\end{matrix}\right.\)

Mà a > 0 nên \(a=2\)

\(\Rightarrow\sqrt{x}+\sqrt{2-x}=2\)

\(\Leftrightarrow x+2-x+2\sqrt{x\left(2-x\right)}=2\)

\(\Leftrightarrow2\sqrt{x\left(2-x\right)}=0\)

\(\Leftrightarrow x\left(2-x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(tmdk\right)\\x=2\left(tmdk\right)\end{matrix}\right.\)

Vậy ...

Thay m=-4 vào (1), ta được:

\(x^2+x-4-2=0\)

=>\(x^2+x-6=0\)

=>(x+3)(x-2)=0

=>\(\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)

tìm m để phương trình (1) có hai nghiệm x1,x2 thỏa mãn \(x1^2+2x1.x2-x2-1=0\) giúp e luon ạ

 a) Ta có \(VT=cot^2\alpha+1=\dfrac{cos^2\alpha}{sin^2\alpha}+1\) \(=\dfrac{cos^2\alpha+sin^2\alpha}{sin^2\alpha}\) \(=\dfrac{1}{sin^2\alpha}\) \(=VP\), vậy đẳng thức được chứng minh.

 b) \(cot\alpha=3\Rightarrow tan\alpha=\dfrac{1}{3}\) (do \(tan\alpha.cot\alpha=1\))

 Có \(\dfrac{1}{sin^2\alpha}=1+cot^2\alpha=1+3^2=10\) \(\Rightarrow sin^2\alpha=\dfrac{1}{10}\) \(\Rightarrow sin\alpha=\dfrac{1}{\sqrt{10}}\)

 Lại có \(sin^2\alpha+cos^2\alpha=1\) \(\Rightarrow cos\alpha=\sqrt{1-sin^2\alpha}=\sqrt{1-\left(\dfrac{1}{\sqrt{10}}\right)^2}=\dfrac{3}{\sqrt{10}}\) 

a) cot²∝ + 1

= cos²∝/sin²∝ + 1

= (cos²∝ + sin²∝)/sin²∝

= 1/sin²∝

b) cot∝ = 3

⇒ cot²∝ + 1 = 10

⇒ 1/sin²∝ = 10

⇒ sin²∝ = 1/10

⇒ sin∝ = √10/10 (do nhọn)

Lại có:

sin²∝ + cos²∝ = 1

⇒ cos²∝ = 1 - sin²∝

= 1 - 1/10

= 9/10

⇒ cos∝ = 3√10/10

cot∝ = 3

⇒ tan∝ = 1/3

a: \(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\)

=>\(cot^2\alpha=1:\dfrac{1}{9}-1=9-1=8\)

=>\(cot\alpha=2\sqrt{2}\)

=>\(tan\alpha=\dfrac{1}{2\sqrt{2}}=\dfrac{\sqrt{2}}{4}\)

b: \(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)

=>\(1+tan^2\alpha=1:\left(\dfrac{2}{\sqrt{5}}\right)^2=\dfrac{5}{4}\)

=>\(tan^2\alpha=\dfrac{1}{4}\)

=>\(tan\alpha=\dfrac{1}{2}\)

Câu 3.2

Để pt có 2 nghiệm pb thì:

$\Delta=(2m+3)^2+4(2m+4)>0$

$\Leftrightarrow (2m+3)^2+4(2m+3)+4>0$

$\Leftrightarrow (2m+3+2)^2>0\Leftrightarrow (2m+5)^2>0$

$\Leftrightarrow 2m+5\neq 0$

$\Leftrightarrow m\neq \frac{-5}{2}$

Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm của pt (1) thì:

$x_1+x_2=2m+3$

$x_1x_2=-2m-4$

$\Rightarrow x_1+x_2+x_1x_2+1=0$

$\Leftrightarrow (x_1+1)(x_2+1)=0$

$\Leftrightarrow x_1=-1$ hoặc $x_2=-1$

Nếu $x_1=-1$ thì $x_2=2m+4$. Nếu $x_2=-1$ thì $x_1=2m+4$

Không mất tổng quát giả sử $x_1=-1; x_2=2m+4$

Khi đó:

$|x_1|+|x_2|=5$

$\Leftrightarrow |-1|+|2m+4|=5$

$\Leftrightarrow |2m+4|=4$

$\Leftrightarrow 2m+4=\pm 4$

$\Leftrightarrow m=0$ hoặc $m=-4$

Do $m> \frac{-5}{2}$ nên $m=0$