Cho tập hợp A ={ 0;2;4;6;8;10;12;14}. Hãy viết Tập A theo tính chất đặc trưng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có: \(\widehat{M}=\widehat{N}\)
=>AM//BN
Ta có: AM//BN
=>\(\widehat{A_1}+\widehat{B_1}=180^0\)
mà \(2\widehat{A_1}=3\cdot\widehat{B_1}\)
nên \(\widehat{B_1}=180^0\cdot\dfrac{2}{5}=72^0\)
Ta có: \(\widehat{B_1}+\widehat{B_2}=180^0\)(hai góc kề bù)
=>\(\widehat{B_2}+72^0=180^0\)
=>\(\widehat{B_2}=108^0\)
\(\widehat{B_3}=\widehat{B_1}\)(hai góc đối đỉnh)
mà \(\widehat{B_1}=72^0\)
nên \(\widehat{B_3}=72^0\)


Gọi hai số cần tìm là a,b
Hai số có tỉ số bằng 2:5 nên \(\dfrac{a}{b}=\dfrac{2}{5}\)
=>a=0,4b
Nếu thêm 16 đơn vị vào số thứ nhất và bớt đi 16 đơn vị ở số thứ hai thì hai số mới có tỉ số là 3:4 nên \(\dfrac{a+16}{b-16}=\dfrac{3}{4}\)
=>4a+64=3b-48
=>1,6+64=3b-48
=>-1,4=-112
=>b=80
=>\(a=2,5\cdot80=200\)
Vậy: Hai số cần tìm là 200;80

a: Xét tứ giác BHCK có
M là trung điểm chung của BC và HK
=>BHCK là hình bình hành
b: BHCK là hình bình hành
=>BH//CK và BK//CH
Ta có: BH//CK
BH\(\perp\)AC
DO đó: CK\(\perp\)AC
Ta có:BK//CH
CH\(\perp\)AB
Do đó: BK\(\perp\)BA
c: ΔBEC vuông tại E
mà EM là đường trung tuyến
nên \(EM=\dfrac{BC}{2}\left(1\right)\)
Ta có: ΔBFC vuông tại F
mà FM là đường trung tuyến
nên \(FM=\dfrac{BC}{2}\left(2\right)\)
Từ (1),(2) suy ra ME=MF
=>ΔMEF cân tại M

a: Diện tích đáy là: \(S_{ABC}=\dfrac{1}{2}\cdot4\cdot10=20\left(cm^2\right)\)
Thể tích lăng trụ đứng là \(V=20\cdot8=160\left(cm^3\right)\)
b: Thể tích lưỡi rìu là \(160\cdot90\%=144\left(cm^3\right)=0,144\left(dm^3\right)\)
Khối lượng lưỡi rìu là:
\(0,144\cdot7,87=1,13328\left(kg\right)\)

Khối lượng đường ngày thứ nhất cửa hàng bán được là:
\(235,5\times\dfrac{3}{10}=70,65\left(kg\right)\)
Khối lượng đường còn lại là 235,5-70,65=164,85(kg)
Khối lượng đường ngày thứ hai bán được là:
164,85x0,7=115,395(kg)
Khối lượng đường ngày thứ ba bán được là:
164,85-115,395=49,455(kg)

Vì \(\widehat{xOy}\ne180^0\)
nên Ox không song song với Oy
Vì a//Ox
và Ox không song song với Oy
nên a luôn cắt Oy

\(1,A=x^2-12x+11\\ =\left(x^2-12x+36\right)-25\\ =\left(x-6\right)^2-25\)
Ta có: `(x-6)^2>=0` với mọi x
`=>(x-6)^2-25>=-25` với mọi x
Dấu "=" xảy ra: `x-6=0<=>x=6`
\(2,M=-4x^2+12x-7\\ =\left(-4x^2+12x-9\right)+2\\ =-\left(4x^2-12x+9\right)+2\\ =-\left(2x-3\right)^2+2\)
Ta có: `(2x-3)^2>=0` với mọi x
`=>-(2x-3)^2<=0` với mọi x
`=>-(2x-3)^2+2<=2` với mọi x
Dấu "=" xảy ra: `2x-3=0<=>x=3/2`
1: \(A=x^2-12x+11\)
\(=x^2-12x+36-25\)
\(=\left(x-6\right)^2-25>=-25\forall x\)
Dấu '=' xảy ra khi x-6=0
=>x=6
10: \(M=-4x^2+12x-7\)
\(=-4x^2+12x-9+2\)
\(=-\left(2x-3\right)^2+2< =2\forall x\)
Dấu '=' xảy ra khi 2x-3=0
=>2x=3
=>\(x=\dfrac{3}{2}\)
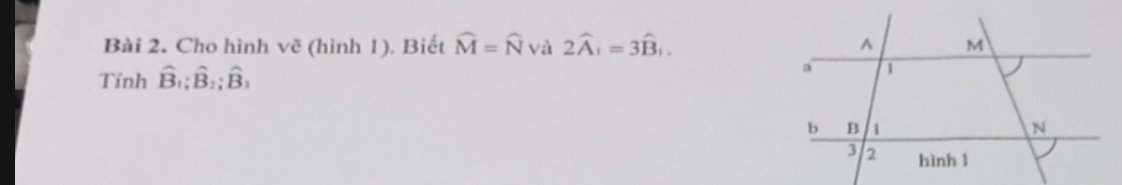


A={x\(\in\)N|x=2k; 0<=k<=7}