3/1x2 + 3/2x3 + 3/3x4 + ..... 3/2021x2022
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-2\right).\left(x-2\right)+2024=\left(x-2\right)^2+2024\ge2024\forall x\in R\\ Vậy:min_{BT}=2024\Leftrightarrow x-2=0\Leftrightarrow x=2\)

Lời giải:
$\frac{3}{1\times 3}+\frac{3}{3\times 5}+\frac{3}{5\times 7}+....+\frac{3}{57\times 59}$
$=\frac{3}{2}(\frac{3-1}{1\times 3}+\frac{5-3}{3\times 5}+\frac{7-5}{5\times 7}+....+\frac{59-57}{57\times 59})$
$=\frac{3}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{57}-\frac{1}{59})$
$=\frac{3}{2}(1-\frac{1}{59})=\frac{87}{59}$
Sửa đề: \(\dfrac{3}{1.3}+\dfrac{3}{3.5}+...+\dfrac{3}{57.59}\)
\(=\dfrac{3}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{57.59}\right)\)
\(=\dfrac{3}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{57}-\dfrac{1}{59}\right)\)
\(=\dfrac{3}{2}.\left(1-\dfrac{1}{59}\right)\)
\(=\dfrac{3}{2}.\dfrac{58}{59}=\dfrac{87}{59}\)

Suy nghĩ về công lao của cha mẹ, tôi hiểu rằng họ là những người hiến dâng tất cả cho con cái với tình thương vô bờ. Cha mẹ là những người vất vả làm việc, hy sinh và kiên nhẫn dạy dỗ, để cho con có cuộc sống tốt đẹp hơn. Thương cha nhớ mẹ không chỉ là sự nhớ nhung về hình ảnh của họ, mà còn là việc gìn giữ và trân trọng những giá trị mà họ đã truyền đạt cho chúng ta. Sự hiện diện và tình thương của cha mẹ là nguồn động viên lớn lao trong cuộc sống, là nền tảng vững chắc để chúng ta vươn lên và thành công. Mỗi khi thương cha nhớ mẹ, tôi cảm nhận được lòng biết ơn sâu sắc và quyết tâm sống đáng giá để trả công cho họ.

Lời giải:
Đặt $A=\frac{1}{20.23}+\frac{1}{23.26}+\frac{1}{26.29}+...+\frac{1}{77.80}$
$3A=\frac{3}{20.23}+\frac{3}{23.26}+\frac{3}{26.29}+...+\frac{3}{77.80}$
$=\frac{23-20}{20.23}+\frac{26-23}{23.26}+\frac{29-26}{26.29}+...+\frac{80-77}{77.80}$
$=\frac{1}{20}-\frac{1}{23}+\frac{1}{23}-\frac{1}{26}+\frac{1}{26}-\frac{1}{29}+...+\frac{1}{77}-\frac{1}{80}$
$=\frac{1}{20}-\frac{1}{80}$
$A=\frac{1}{3}(\frac{1}{20}-\frac{1}{80})=\frac{1}{60}-\frac{1}{240}< \frac{1}{60}< \frac{1}{9}$
Ta có:
\(\dfrac{1}{20.23}+\dfrac{1}{23.26}+...+\dfrac{1}{77.80}\)
\(=\dfrac{1}{3}\left(\dfrac{3}{20.23}+\dfrac{3}{23.26}+...+\dfrac{3}{77.80}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{20}-\dfrac{1}{23}+\dfrac{1}{23}-\dfrac{1}{26}+...+\dfrac{1}{77}-\dfrac{1}{80}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{20}-\dfrac{1}{80}\right)\)
\(=\dfrac{1}{3}.\dfrac{3}{80}=\dfrac{1}{80}< \dfrac{1}{9}\) (đpcm)

A = 5 + 52 + 53 + ... + 5100
5A = 52 + 53 + 54 + ... + 5101
5A - A = (52 + 53 + 54 + ... + 5101) - (52 + 53 + 54 + ... + 5100)
4A = 52 + 53 + 54 + ... + 5101 - 52 - 53 - 54 - ... - 5100
4A = (52 - 52) + (53 - 53) + (54 - 54) + ... + (5100 - 5100) + (5101 - 5)
4A = 0 + 0 + ... 0 + 5101 - 5
A = \(\dfrac{5^{101}-5}{4}\)
b; 4.A + 5 = 5n
5101 - 5 + 5 = 5n
5101 = 5n
n = 101
Vậy n = 101

Lời giải:
a. Sau 1 năm Trúc nhận được số tiền cả vốn lẫn lãi là:
$10000000+10000000\times 6:100=10600000$ (đồng)
b. Nếu bạn chỉ gửi tiền với lãi suất không kỳ hạn thì sau 40 ngày bạn nhận tổng cộng:
$10000000+10000000\times \frac{0,3}{100}\times \frac{40}{365}=10003287$ (đồng)

Lời giải:
Cần thêm số nước để đầy bể là:
$1-\frac{3}{4}=\frac{1}{4}$ (dung tích bể)
Vòi chảy đầy bể sau: $\frac{1}{4}: \frac{1}{8}=2$ (giờ)
Thời gian vòi chảy đầy bể là:
\(\dfrac{3}{4}:\dfrac{1}{8}=6\) (giờ)
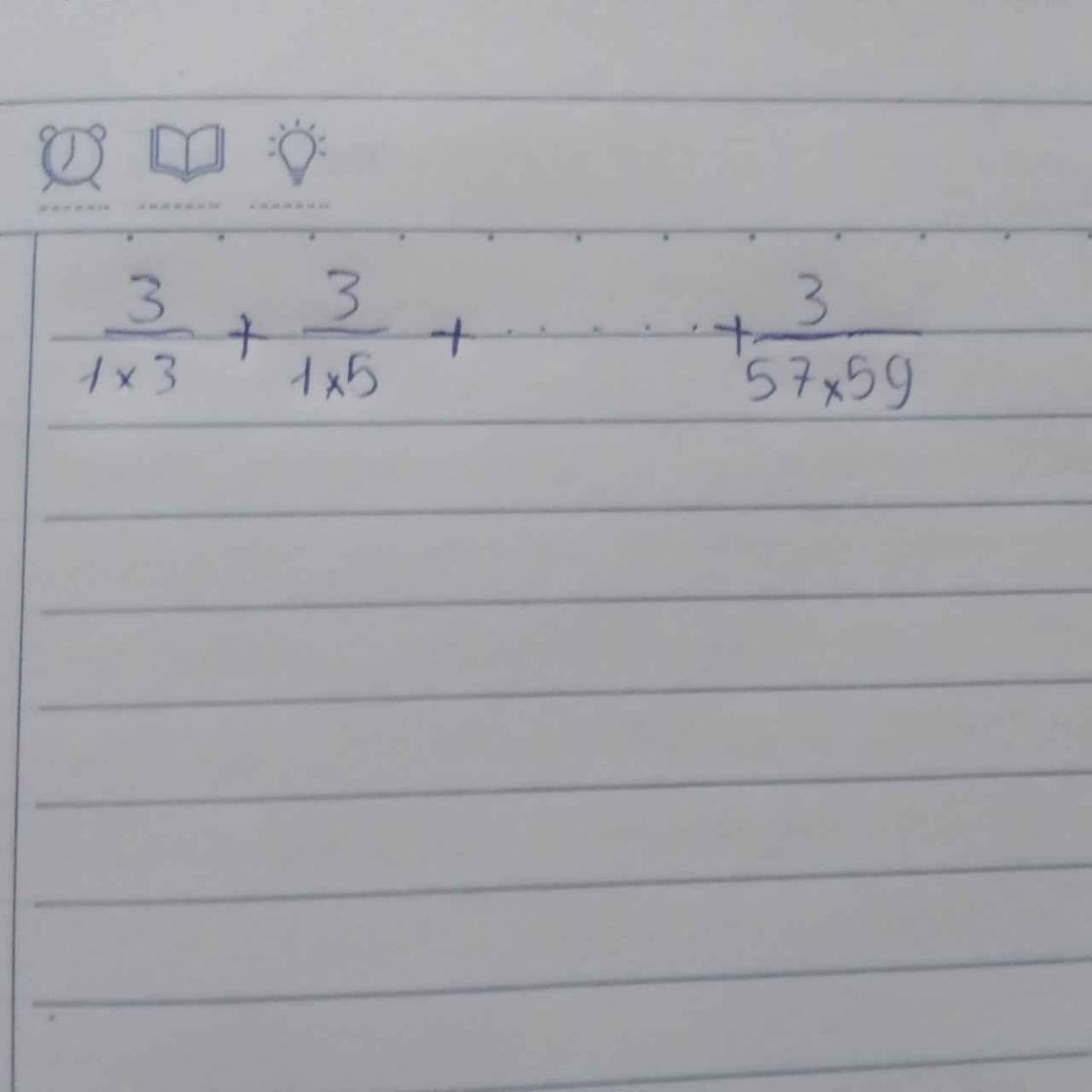

\(\dfrac{3}{1.2}+\dfrac{3}{2.3}+\dfrac{3}{3.4}+...+\dfrac{3}{2021.2022}\)
\(=3\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2021.2022}\right)\)
\(=3.\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\right)\)
\(=3.\left(1-\dfrac{1}{2022}\right)\)
\(=\dfrac{2021}{674}\)