Số phần tử của tập hợp Q= {1972;1973;1974;1975;.....;2011 là:
A. 37 phần tử
B. 40 phần tử
C. 29 phần tử
D. 41 phần tử
E. 36 phần tử
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu anh Dũng đi bộ từ A đến B thì hết thời gian là:
\(19:6=\dfrac{19}{6}\) (giờ) = 3 giờ 10 phút
Nếu anh Dũng đi bộ từ A đến B thì đến nơi lúc:
6 giờ 30 phút + 3 giờ 10 phút = 9 giờ 40 phút
Vì anh Dũng lên xe máy đi một đoạn đường nên đến sớm hơn là:
9 giờ 40 phút - 8 giờ = 1 giờ 40 phút = 100 phút
Tỉ số giữa vận tốc đi bộ và vận tốc đi xe máy của anh Dũng là:
\(6:30=\dfrac{1}{5}\)
Tỉ số thời gian đi bộ và thời gian đi xe máy của anh Dũng là:
\(1:\dfrac{1}{5}=5\)
Thời gian đi xe máy của anh Dũng là:
\(100:\left(5-1\right)=25\) (phút) \(=\dfrac{5}{12}\) giờ
Quảng đường anh Dũng đã đi xe máy là:
\(30\times\dfrac{5}{12}=12,5\left(km\right)\)
Quảng đường anh Dũng đã đi bộ là:
\(19-12,5=6,5\left(km\right)\)
Đáp số:...
Đây là toán nâng cao chuyên đề chuyển động, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp giả thiết tạm như sau:
Giải:
Thời gian anh Dũng đi từ huyện A đến huyện B là:
8 giờ - 6 giờ 30 phút = 1 giờ 30 phút
1 giờ 30 phút = 1,5 giờ
Nếu anh Dũng đi bằng xe máy trong 1,5 giờ thì quãng đường mà anh đi được so với thực tế thì thừa ra là: 30 x 1,5 - 19 = 26 (km)
Cứ một giờ đi xe máy thay bằng đi bộ thì quãng đường giảm là: 30 - 6 = 24 (km)
Thời gian anh Dũng đi bộ là: 26 : 24 = \(\dfrac{13}{12}\) (giờ)
Quãng đường mà anh Dũng đã đi bộ là: 6 x \(\dfrac{13}{12}\) = 6,5 (km)
Đáp số: 6,5km

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=\dfrac{\left(bd\right)\cdot k^2}{bd}=k^2\left(1\right)\)
\(VP=\dfrac{2009a^2+2010c^2}{2009b^2+2010d^2}=\dfrac{2009\cdot\left(bk\right)^2+2010\cdot\left(dk\right)^2}{2009b^2+2010d^2}\\ =\dfrac{2009b^2\cdot k^2+2010d^2\cdot k^2}{2009b^2+2010d^2}=\dfrac{k^2\cdot\left(2009b^2+2010d^2\right)}{2009b^2+2010d^2}\\ =k^2\left(2\right)\)
Từ (1) và (2) => \(\dfrac{ac}{bd}=\dfrac{2009a^2+2010c^2}{2009b^2+2010d^2}\)

Đổi: 45 phút = \(\dfrac{3}{4}\) giờ; 54 phút = \(\dfrac{9}{10}\) giờ
Độ dài quãng đường AB là:
\(48\times\dfrac{3}{4}=36\left(km\right)\)
Vận tốc của thuyền lúc ngược dòng là:
\(36:\dfrac{9}{10}=40\left(km\text{/}h\right)\)
Vận tốc của dòng nước là:
\(\left(48-40\right):2=4\left(km\text{/}h\right)\)
Đáp số: 40 km/h
Giải:
45 phút = \(\dfrac{3}{4}\) giờ; 54 phút = \(\dfrac{9}{10}\) giờ
Quãng sông AB dài là: 48 x \(\dfrac{3}{4}\) = 36 (km)
Vận tốc thuyền khi ngược dòng là: 36 : \(\dfrac{9}{10}\) = 40 (km/h)
Vận tốc dòng nước là: (48 - 40): 2 = 4 (km/h)
Đáp số:....

B5:
a) Thay x = 1 và y = 2 vào pt ta có:
\(m\cdot1+2-5=0\\ =>m-3=0\\ =>m=3\)
b) A(0;3) thuộc đường thẳng 4x - my - 6 = 0
=> Thay x = 0 và y = 3 vào đường thẳng ta có:
\(4\cdot0-m\cdot3-6=0\\ =>0-3m-6=0\\=> -3m-6=0\\ =>-3m=6\\ =>m=\dfrac{6}{-3}=-2\)
B11:
Ta có:
\(\left\{{}\begin{matrix}2x+3y=7\\x-3y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=6\\x-3y=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{6}{3}=2\\2-3y=-1\end{matrix}\right. \Leftrightarrow\left\{{}\begin{matrix}x=2\\3y=2+1=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{3}{3}=1\end{matrix}\right.\)
=> Cặp (2;1) là nghiệm của hpt
B12:
Ta có
\(\left\{{}\begin{matrix}4x+5y=3\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+5y=3\\4x-12y=20\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}17y=-17\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-17}{17}=-1\\x+3=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=5-3=2\end{matrix}\right.\)
=> Cặp (2;-1) là nghiệm của hpt

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{a^2+ac}{c^2-ac}=\dfrac{\left(bk^2\right)+bk\cdot dk}{\left(dk\right)^2-bk\cdot dk}\\ =\dfrac{b^2k^2+bdk^2}{d^2k^2-bdk^2}=\dfrac{k^2\left(b^2+bd\right)}{k^2\left(d^2-bd\right)}=\dfrac{b^2+bd}{d^2+bd}=VP\)

\(\dfrac{a}{b}=\dfrac{b}{d}=>b^2=ad\)
Ta có:
\(VT=\dfrac{a^2+b^2}{b^2+d^2}=\dfrac{a^2+ad}{ad+d^2}=\dfrac{a\left(a+d\right)}{d\left(a+d\right)}=\dfrac{a}{d}=VP\)

\(4y^4+1\\ =4y^4+4y^2+1-4y^2\\ =\left(4y^4+4y^2+1\right)-4y^2\\ =\left(2y^2+1\right)^2-\left(2y\right)^2\\ =\left(2y^2-2y+1\right)\left(2y^2+2y+1\right)\)
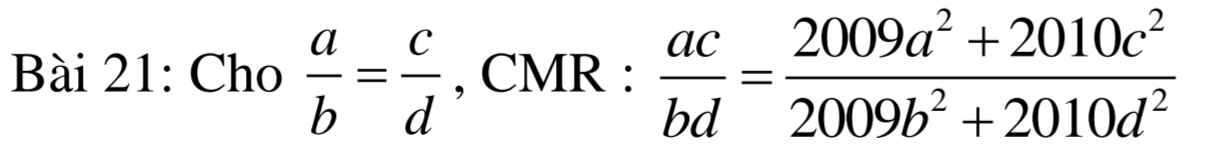





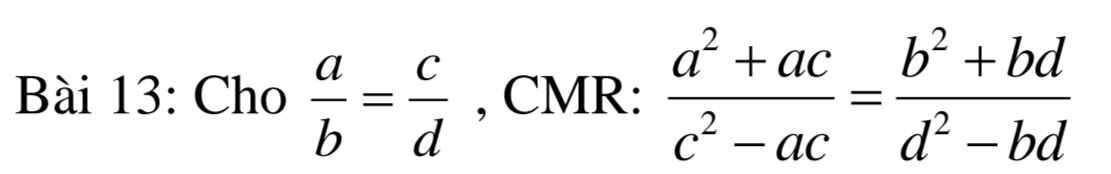
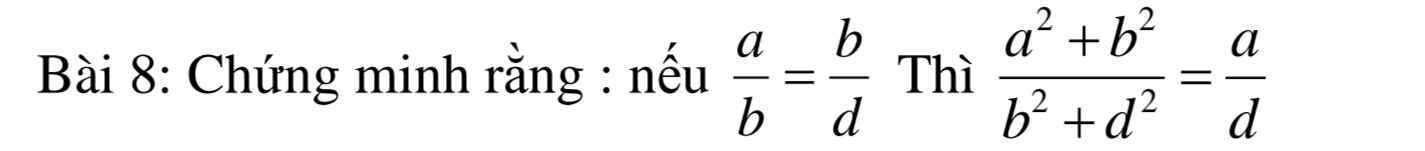
Số phần tử của tập hợp Q là:
(2011 - 1972) : 1 + 1 = 40 (phần tử)
=> Chọn B
\(\left|Q\right|=2011-1972+1=40\)