Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số số hạng là \(\dfrac{2x-1-1}{2}+1=\dfrac{2x-2}{2}+1=x\left(số\right)\)
Tổng của dãy số là \(\dfrac{x\left(2x-1+1\right)}{2}=x^2\)
Do đó, ta có: \(x^2=225\)
=>\(\left[{}\begin{matrix}x=15\left(nhận\right)\\x=-15\left(loại\right)\end{matrix}\right.\)
Vậy: x=15

(1,1 + 1,2 x 1,3 + 1,4 x 1,5 + 1,6 x 1,7 + 1,8 x 1,9) x (1,25 - 0,25 x 5)
= (1,1 + 1,2 x 1,3 + 1,4 x 1.5 + 1,6 x 1,7 + 1,8 x 1,9) x (1,25 - 1,25)
= (1,1 + 1,2 x 1,3 + 1,4 x 1,5 + 1,6 x 1,7 + 1,8 x 1,9) x 0
= 0
(1,1 + 1,2 + 1,3 + 1,4 + 1,5 + 1,6 + 1,7 + 1,8 + 1,9) × (1,25 - 0,25 × 5)
= (1,1 + 1,2 + 1,3 + 1,4 + 1,5 + 1,6 + 1,7 + 1,8 + 1,9) × 0
= 0

Lời giải:
a.
Đơn thức:
$\frac{4}{5}x$: hệ số $\frac{4}{5}$, phần biến $x$
$(\sqrt{2}-1)xy$: hệ số $\sqrt{2}-1$, phần biến $xy$
$-3xy^2$: hệ số $-3$, phần biến $xy^2$
$\frac{1}{2}x^2y$: hệ số $\frac{1}{2}$, phần biến $x^2y$
$\frac{1}{x}y^3$: hệ số $1$, phần biến $\frac{1}{x}y^3$
$\frac{-3}{2}x^2y$: hệ số $\frac{-3}{2}$, phần biến $x^2y$
Các biểu thức còn lại không phải đơn thức.
c.
Gọi đa thức là $A(x)$
$A(x)=\frac{4}{5}x+(\sqrt{2}-1)xy-3xy^2+\frac{1}{2}x^2y+\frac{1}{x}y^3+\frac{-3}{2}x^2y$
$=\frac{4}{5}x+(\sqrt{2}-1)xy-3xy^2-x^2y+\frac{1}{x}y^3$
Bậc: $3$

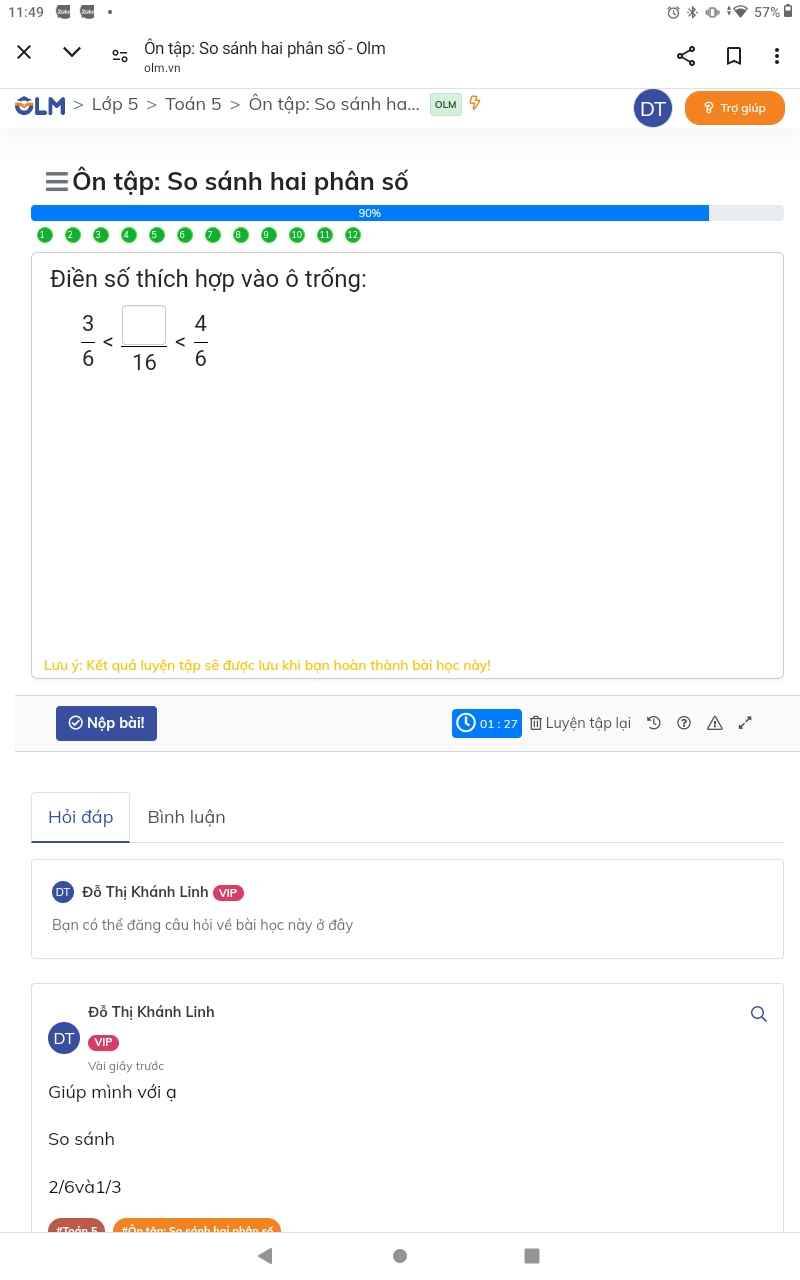
\(\dfrac{3}{6}\) < \(\dfrac{◻}{16}\) < \(\dfrac{4}{6}\)
\(\dfrac{3\times8}{6\times8}\) < \(\dfrac{◻\times3}{16\times3}\) < \(\dfrac{4\times8}{6\times8}\)
\(\dfrac{24}{48}\) < \(\dfrac{◻\times3}{48}\) < \(\dfrac{32}{48}\)
24 < \(◻\) \(\times\) 3 < 32
\(\dfrac{24}{3}\) < \(◻\) < \(\dfrac{32}{3}\)
8 < \(◻\) < 10 \(\dfrac{2}{3}\)
\(◻\) = 9; 10
\(\dfrac{2}{6}\) = \(\dfrac{2:2}{6:2}=\dfrac{1}{3}\)
Vậy \(\dfrac{2}{6}\) = \(\dfrac{1}{3}\)

Hiệu số phần bằng nhau là 5-2=3(phần)
Số lớn là 204:3x5=340
Số bé là 340-204=136

Từ mẫu số của các phân số trên, ta có dãy:
8; 15; 24; 35; ...
2 x 4; 3 x 5; 4 x 6; 5 x 7;...
Do không chứa 1 (số đầu của dãy gốc) nên ta chỉ cần tìm đến số thứ 47 của dãy các mẫu số.
Nhận xét: Mỗi thừa số cách nhau 2 đơn vị và thừa số đầu/cuối của tích trước cách thừa số đầu/cuối của tích sau là 1 đơn vị.
Từ 1 - 47 có 47 số ⇒ từ 2 - 47 có 46 số và thừa số đầu tiên của tích số cuối cùng của dãy sẽ là: 46 và số tiếp theo sẽ là: 48
⇒ Số thứ 47 của dãy chứa mẫu số là:
46 x 48 = 2208
Vậy số thứ 48 của dãy ban đầu là: 1/2208
Đáp số: 1/2208
Bạn nhấn vào biểu tượng Σ để nhập phân số hoặc công thức trong toán học nhé!

\(\dfrac{8}{9}\div x+\dfrac{4}{9}\times\dfrac{1}{3}=3\dfrac{1}{3}\)
\(\dfrac{8}{9}\div x+\dfrac{4}{27}=\dfrac{10}{3}\)
\(\dfrac{8}{9}\div x=\dfrac{10}{3}-\dfrac{4}{27}\)
\(\dfrac{8}{9}\div x=\dfrac{86}{27}\)
\(x=\dfrac{8}{9}\div\dfrac{86}{27}\)
\(x=\dfrac{8}{9}\times\dfrac{27}{86}\)
\(x=\dfrac{12}{43}\)
Vậy \(x=\dfrac{12}{43}\)
\(\dfrac{8}{9}:x+\dfrac{4}{9}\times\dfrac{1}{3}=3\dfrac{1}{3}\)
=>\(\dfrac{8}{9}:x=\dfrac{10}{3}-\dfrac{4}{27}=\dfrac{90}{27}-\dfrac{4}{27}=\dfrac{86}{27}\)
=>\(x=\dfrac{8}{9}:\dfrac{86}{27}=\dfrac{8}{9}\times\dfrac{27}{86}=\dfrac{4}{43}\times3=\dfrac{12}{43}\)

Bài 6:
\(A=ax+bx+3ay+3by\)
\(=x\left(a+b\right)+3y\left(a+b\right)\)
\(=\left(a+b\right)\left(x+3y\right)=5\cdot7=35\)
Bài 7:
a: \(\left(2x-4\right)^2>=0\forall x\)
\(\left(3y-9\right)^4>=0\forall y\)
Do đó: \(\left(2x-4\right)^2+\left(3y-9\right)^4>=0\forall x,y\)
mà \(\left(2x-4\right)^2+\left(3y-9\right)^4< =0\forall x,y\)
nên \(\left\{{}\begin{matrix}2x-4=0\\3y-9=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
b; (\(x^3\) - 1)(\(x^3\) - 10)(\(x^3\) - 30)(\(x^3\) - 70) < 0
Đặt \(x^3\) = t
Khi đó: T = (t - 1)(t - 10)(t - 30)(t - 70) < 0
Lập bảng xét dấu ta có:
| t | 1 10 30 70 |
| t - 1 | - 0 + + + + |
| t - 10 | - - 0 + + + |
| t - 30 | - - - 0 + + |
| t - 70 | - - - - 0 + |
| T = (t - 1).(t - 10).(t - 30).(t - 70) | + 0 - 0 + 0 - 0 + |
Theo bảng trên ta có:
1 < t < 10 hoặc 30 < t < 70
⇒ 1 < \(x^3\) - 1 < 10 ⇒ 2 < \(x^3\) < 11
Vì \(x\) nguyên nên \(x\)3 = 8 ⇒ \(x^3\) = 23 ⇒ \(x=2\)
30 < t < 70
30 < \(x^3\) - 1 < 70
31 < \(x^3\) < 71
Vì \(x\) nguyên nên \(x^3\) = 64
⇒ \(x^3\) = 43 ⇒ \(x\) = 4
Vậy \(x\) \(\in\) {2; 4}
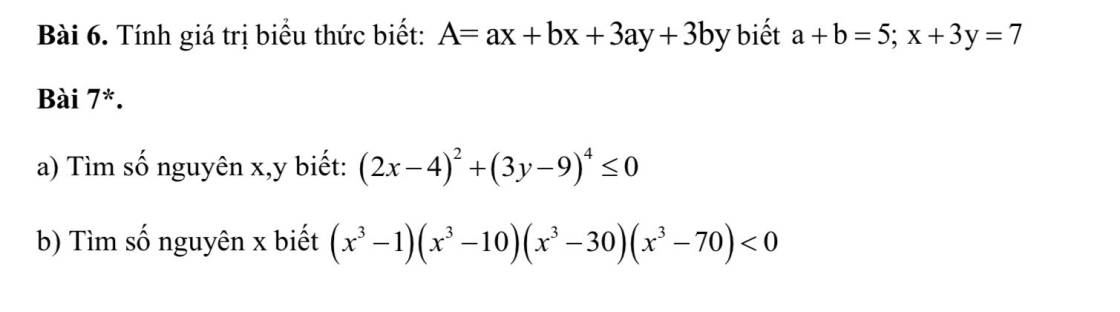
a: \(CD=3\times AB=54\left(cm\right)\)
\(AH=\dfrac{2}{3}\times18=12\left(cm\right)\)
Diện tích hình thang ABCD là:
\(S_{ABCD}=\dfrac{1}{2}\times\left(AB+CD\right)\times AH=\dfrac{1}{2}\times12\times\left(54+18\right)=72\times6=432\left(cm^2\right)\)
Vì AB//CD
nên \(\dfrac{S_{ABD}}{S_{BDC}}=\dfrac{AB}{DC}=\dfrac{1}{3}\)
=>\(S_{BDC}=3\times S_{ABD}\)
mà \(S_{ABD}+S_{BDC}=S_{ABCD}=432\)
nên \(S_{ABD}=\dfrac{432}{4}=108\left(cm^2\right)\)
=>\(S_{BDC}=432-108=324\left(cm^2\right)\)
b: Vì AB//CD
nên \(\dfrac{OA}{OC}=\dfrac{AB}{CD}=\dfrac{1}{3}\)
=>\(\dfrac{S_{AOB}}{S_{BOC}}=\dfrac{OA}{OC}=\dfrac{1}{3}\)
=>\(S_{BOC}=3\times S_{AOB}\)
=>\(S_{BOC}>S_{AOB}\)
c: \(\dfrac{OA}{OC}=\dfrac{1}{3}\)
=>OC=3OA
=>OC>OA
vẽ cả hình