a: Chiều cao hạ từ đỉnh A là:

\(\dfrac{3}{4}\times12=9\left(km\right)\)

Diện tích tam giác ABC là: \(S=\dfrac{1}{2}\times12\times9=54\left(km^2\right)\)

b: \(AM=\dfrac{1}{3}MC\)

=>\(AM=\dfrac{1}{4}AC\)

=>\(CM=\dfrac{3}{4}CA\)

=>\(S_{BMC}=\dfrac{3}{4}\times S_{ABC}=40,5\left(km^2\right)\)

mình nghĩ là 14 hình

1+2+3+4+5+6=21hình

a: Số cần tìm là 400:25%=400:0,25=1600

b: Số cần tìm là 150:12%=150:0,12=1250

c: Số cần tìm là 45:75%=45:0,75=60

d: Số cần tìm là 54:1,8%=54:0,018=3000

e: Số cần tìm là 31:62%=31:0,62=50

g: Số cần tìm là 42:70%=60

a)400:25x100=1600

b)150:12x100=1250

c)45:75x100=60

d)54:1,8x100=3000

e)31:62x100=50

g)42:70x100=60

a 400:100×15=60

b $130:100\times 12,5=16,25$ $\left(kg\right)$

$c$$125:100\times 24=30$ $\left(m^2\right)$

$d$$720:100\times 0,2=1,44$ $\left(m\right)$

$e$$172:100\times 6=10,32$ $\left(d{m}^2\right)$

$g$$1200:100\times 5=60$ $($ cây$)$

a)400:100x15=60

b)130:100x12,5=16,25kg

c)125:100x24=30m\(^2\)

d)720:100x0,2=1,44dm\(^2\)

e)172:100x6=10,32 cái cây

g)1200:100x5=60 cái cây

ĐKXĐ: $x\notin\{-5;-4;-3\}$

$\frac{1}{x+5}+\frac{2}{x+4}+\frac{3}{x+3}+3=0$

$\Leftrightarrow \left(\frac{1}{x+3}+1\right)+\left(\frac{2}{x+4}+1\right)+\left(\frac{3}{x+3}+1\right)=0$

$\Leftrightarrow \frac{x+6}{x+5}+\frac{x+6}{x+4}+\frac{x+6}{x+3}=0$

$\Leftrightarrow (x+6)\left(\frac{1}{x+5}+\frac{1}{x+4}+\frac{1}{x+3}\right)=0$

+, TH1: $x+6=0\Leftrightarrow x=-6$ (tm ĐKXĐ)

+, TH2: $\frac{1}{x+5}+\frac{1}{x+4}+\frac{1}{x+3}=0$

$\Leftrightarrow \frac{(x+4)(x+3)+(x+3)(x+5)+(x+4)(x+5)}{(x+3)(x+4)(x+5)}=0$

$\Rightarrow 3x^2+24x+47=0$

$\Leftrightarrow \left[\begin{array}{}x =\frac{-12+\sqrt3}{3}(TM) \\x=\frac{-12-\sqrt3}{3}(TM) \end{array}\right. $

$\text{#}Toru$

ĐKXĐ: \(x\notin\left\{-5;-4;-3\right\}\)

\(\dfrac{1}{x+5}+\dfrac{2}{x+4}+\dfrac{3}{x+3}+3=0\)

=>\(\left(\dfrac{1}{x+5}+1\right)+\left(\dfrac{2}{x+4}+1\right)+\left(\dfrac{3}{x+3}+1\right)=0\)

=>\(\dfrac{x+6}{x+5}+\dfrac{x+6}{x+4}+\dfrac{x+6}{x+3}=0\)

=>\(\left(x+6\right)\left(\dfrac{1}{x+5}+\dfrac{1}{x+4}+\dfrac{1}{x+3}\right)=0\)

=>x+6=0

=>x=-6(nhận)

Gọi phân số đó là \(x\)

Ta có:

\(\left(x-\dfrac{5}{4}\right):3+\dfrac{1}{4}=2\)

\(\left(x-\dfrac{5}{4}\right):3=2-\dfrac{1}{4}\)

\(\left(x-\dfrac{5}{4}\right):3=\dfrac{7}{4}\)

\(x-\dfrac{5}{4}=\dfrac{7}{4}\times3\)

\(x-\dfrac{5}{4}=\dfrac{21}{4}\)

\(x=\dfrac{21}{4}+\dfrac{5}{4}\)

\(x=\dfrac{26}{4}=\dfrac{13}{2}\)

Vậy...

          Đây là toán nâng cao lớp 4, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp giải ngược như sau:

Từ kết quả cuối cùng làm các phép tính ngược lại các phép tính đề bài ban đã cho. 

                                 Giải:

Phân số cần tìm là: (2 - \(\dfrac{1}{4}\)) x 3 + \(\dfrac{5}{4}\) = \(\dfrac{13}{2}\)

Đáp số: \(\dfrac{13}{2}\) 

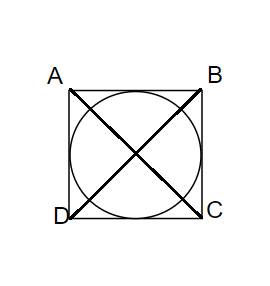
Do 2 đường chéo trên cắt nhau ở chính giữa 2 đường nên độ dài \(\dfrac{1}{2}\)đoạn BD là: 24 : 2 = 12 (cm)

Diện tích hình vuông ABCD là: 24 x 12 : 2 x 2 = 288 (cm²)

⇒ Cạnh hình vuông (đường kính hình tròn) xấp xỉ: 17.

⇒ Bán kính hình tròn xấp xỉ: 17 : 2 = 8,5 (cm)

Diện tích hình tròn xấp xỉ: 8,5 x 8,5 x 3,14 = 226,865 (cm²)

Vậy diện tích phần tô đậm xấp xỉ: 288 - 226,865 = 1,135 (cm²)

*Mình đoán phần xấp xỉ = hình vuông - hình tròn đúng không?

Tô đậm đâu rùi e

Sửa đề:

Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF

a) Chứng minh tam giác  AEF cân

b) vẽ BH vuông góc AE, CK vuông góc AF. CM tam giác EBH bằng tam giác FCK.

Giải

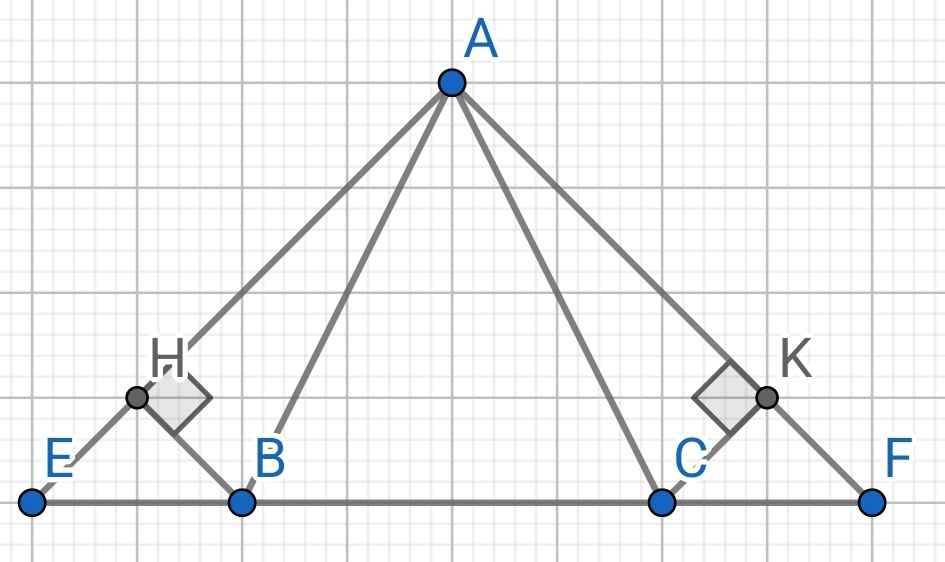
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC và ∠ABC = ∠ACB

Ta có:

∠ABC + ∠ABE = 180⁰ (kề bù)

∠ACB + ∠ACF = 180⁰ (kề bù)

Mà ∠ABC = ∠ACB (cmt)

⇒ ∠ABE = ∠ACF

Xét ∆ABE và ∆ACF có:

AB = AC (cmt)

∠ABE = ∠ACF (cmt)

BE = CF (gt)

⇒ ∆ABE = ∆ACF (c-g-c)

⇒ AE = AF (hai cạnh tương ứng)

⇒ ∆AEF cân tại A

b) Do ∆AEF cân tại A (cmt)

⇒ ∠AEF = ∠AFE

⇒ ∠HEB = ∠KFC

Xét hai tam giác vuông: ∆EBH và ∆FCK có:

BE = CF (gt)

∠HEB = ∠KFC (cmt)

⇒ ∆EBH = ∆FCK (cạnh huyền - góc nhọn)

\(0,75+\dfrac{3}{6}-\dfrac{8}{2}=\dfrac{5}{3}+x.\dfrac{-5}{6}\\ \Rightarrow-\dfrac{5}{6}x=\dfrac{3}{4}+\dfrac{3}{6}-\dfrac{8}{2}-\dfrac{5}{3}\\ \Rightarrow-\dfrac{5}{6}x=\dfrac{9}{12}+\dfrac{6}{12}-\dfrac{48}{12}-\dfrac{20}{12}\\ \Rightarrow-\dfrac{5}{6}x=-\dfrac{53}{12}\\ \Rightarrow x=\left(-\dfrac{53}{12}\right):\left(-\dfrac{5}{6}\right)\\ \Rightarrow x=\dfrac{53}{10}\)

12 - 4 = 8

12 - (-4) = 12 + 4 = 16

-12 - (-4) = -12 + 4 = -8

12 + (-4) = 12 - 4 = 8

15 - (-5) = 15 + 5 = 20

12 - 4 = 8

12 - ( -4) = 12 + 4 = 16

-12 - ( -4) = -12 + 4 = - ( 12 - 4 ) = -8

12 + ( -4) = 12 - 4 =8

15 - ( -5) = 15 + 5 =20