Trong mặt phẳng Oxy cho A(1;2), B(-3;-1), C(4;-2)
1) Viết PTTS đường thẳng AC
2) Viết PTTQ đường thẳng BC
3) Gọi M là trung điểm của AB. Viết PTTS đường thẳng CM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x, y là 2 đại lượng tỉ lệ nghịch nên ta có: \(xy=k=>k=4\cdot1,5=6\)
\(x=0,5=>y=\dfrac{k}{x}=\dfrac{6}{0,5}=12\)
\(x=-1,2=>y=\dfrac{k}{x}=\dfrac{6}{-1,2}=-5\)
\(y=3=>x=\dfrac{k}{y}=\dfrac{6}{3}=2\)
\(y=-2=>x=\dfrac{k}{y}=\dfrac{6}{-2}=-3\)
| x | 0,5 | -1,2 | 2 | -3 | 4 |
| y | 12 | -5 | 3 | -2 | 1,5 |

x và y là 2 đại lượng tỉ lệ nghịch nên: \(xy=k=>k=-2\cdot-15=30\)
\(x=10=>y=\dfrac{k}{x}=\dfrac{30}{10}=3\)
\(y=-3=>x=\dfrac{30}{-3}=-10\)
\(x=15=>y=\dfrac{k}{x}=\dfrac{30}{15}=2\)
\(y=5=>x=\dfrac{k}{y}=\dfrac{30}{5}=6\)
| x | -2 | 10 | -10 | 15 | 6 |
| y | -15 | 3 | -3 | 2 | 5 |

Với \(n=0\) thì đpcm thành \(0⋮30\), luôn đúng.
Với \(n=1\) thì đpcm thành \(x^5-x⋮30\). Ta thấy:
\(VT=x^5-x=x\left(x^4-1\right)=x\left(x^2-1\right)\left(x^2+1\right)=x\left(x-1\right)\left(x+1\right)\left(x^2+1\right)\)
Ta thấy \(x\left(x-1\right)\left(x+1\right)\) là tích của 3 số liên tiếp nên nó chia hết cho 6 \(\Rightarrow VT⋮6\) (1)
Nếu \(x⋮5\Rightarrow VT⋮5\)
Nếu \(x\equiv\pm1\left[5\right]\) thì \(x-1\) hoặc \(x+1\) chia hết cho 5 \(\Rightarrow VT⋮5\)
Nếu \(x\equiv\pm2\left[5\right]\) thì \(x^2+1⋮5\Rightarrow VT⋮5\)
Vậy với mọi \(x\) thì \(VT⋮5\) (2)
Do \(ƯCLN\left(5,6\right)=1\) nên từ (1) và (2) \(\Rightarrow x^5-x⋮30\)
Vậy với \(n=1\) thì khẳng định đúng.
Giả sử khẳng định đúng đến \(n=k\ge0\). Ta cần chứng minh khẳng định đúng với \(n=k+1\)
Với \(n=k+1\), ta có:
\(x^{4n+1}-x\) \(=x^{4\left(k+1\right)+1}-x\)
\(=x^{4k+5}-x\)
\(=x^4.x^{4k+1}-x^5+x^5-x\)
\(=x^4\left(x^{4k+1}-x\right)+\left(x^5-x\right)\)
Mà theo giả thiết quy nạp, \(x^{4k+1}-x⋮30\) và theo cmt thì \(x^5-x⋮30\)
\(\Rightarrow x^{4n+1}-x=x^4\left(x^{4k+1}-x\right)+\left(x^5-x\right)⋮30\). Như vậy, khẳng định đúng với \(n=k+1\).
Theo nguyên lí quy nạp, ta có đpcm.

a) \(\left(-32\right)^9=-32^9=-\left(2^5\right)^9=-2^{45}\)
\(\left(-16\right)^{13}=-16^{13}=-\left(2^4\right)^{13}=-2^{52}\)
Vì \(2^{45}< 2^{52}=>-2^{45}>-2^{52}\)
b) \(\left(-5\right)^{30}=5^{30}=\left(5^3\right)^{10}=125^{10}\)
\(\left(-3\right)^{50}=3^{50}=\left(3^5\right)^{10}=243^{10}\)
Vì \(243>125=>243^{10}>125^{10}>\left(-3\right)^{50}>\left(-5\right)^{30}\)
c) \(\left(\dfrac{1}{2}\right)^{300}=\left[\left(\dfrac{1}{2}\right)^3\right]^{100}=\left(\dfrac{1}{8}\right)^{100}\)
\(\left(\dfrac{1}{3}\right)^{200}=\left[\left(\dfrac{1}{3}\right)^2\right]^{100}=\left(\dfrac{1}{9}\right)^{100}\)
Vì: \(\dfrac{1}{8}>\dfrac{1}{9}=>\left(\dfrac{1}{8}\right)^{100}>\left(\dfrac{1}{9}\right)^{100}=>\left(\dfrac{1}{2}\right)^{300}>\left(\dfrac{1}{3}\right)^{200}\)
d)
\(\left(\dfrac{1}{5}\right)^{199}>\left(\dfrac{1}{5}\right)^{200}=\left[\left(\dfrac{1}{5}\right)^2\right]^{100}\\ =\left(\dfrac{1}{25}\right)^{100}>\left(\dfrac{1}{27}\right)^{100}=\left[\left(\dfrac{1}{3}\right)^3\right]^{100}=\left(\dfrac{1}{3}\right)^{300}\)

Giải:
Khi gấp số bị trừ lên 3 lần thì hiệu mới hơn hiệu cũ là:
1058 - 387 = 671
671 ứng với:
3 - 1 = 2 (lần số bị trừ)
Số bị trừ là:
671 : 2 = \(\dfrac{671}{2}\)
Số trừ là:\(\dfrac{671}{2}\) - 387 = - \(\dfrac{103}{2}\) (lớp 4 chưa học phân số âm)
Không tồn tại số nào thỏa mãn đề bài.

\(\left[\left(-\dfrac{1}{2}\right)^3-\left(\dfrac{3}{4}\right)^3\cdot\left(-2\right)^2\right]:\left[2\cdot\left(-1\right)^5+\left(\dfrac{3}{4}\right)^2-\dfrac{3}{8}\right]\\ =\left(-\dfrac{1}{8}-\dfrac{27}{64}\cdot4\right):\left(2\cdot-1+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(-\dfrac{1}{8}-\dfrac{27}{16}\right):\left(-2+\dfrac{9}{16}-\dfrac{3}{8}\right)\\ =\left(\dfrac{-2}{16}-\dfrac{27}{16}\right):\left(\dfrac{-32}{16}+\dfrac{9}{16}-\dfrac{6}{16}\right)\\ =\dfrac{-29}{16}:\dfrac{-29}{16}\\ =1\)
____________________________
\(\left[3\dfrac{1}{6}-\left(0,06\cdot7\dfrac{1}{2}+6\dfrac{1}{4}\cdot0,24\right)\right]:\left(1\dfrac{2}{3}+2\dfrac{2}{3}\cdot1\dfrac{3}{4}\right)\\ =\left[\dfrac{19}{6}-\left(0,06\cdot\dfrac{15}{2}+\dfrac{25}{4}\cdot4\cdot0,06\right)\right]:\left(\dfrac{5}{3}+\dfrac{8}{3}\cdot\dfrac{7}{4}\right)\\ =\left[\dfrac{19}{6}-0,06\cdot\left(\dfrac{15}{4}+25\right)\right]:\left(\dfrac{5}{3}+\dfrac{14}{3}\right)\\ =\left(\dfrac{19}{6}-0,06\cdot\dfrac{65}{2}\right):\dfrac{19}{3}\\ =\left(\dfrac{19}{6}-\dfrac{39}{20}\right):\dfrac{19}{3}\\ =\dfrac{73}{60}:\dfrac{19}{3}\\ =\dfrac{73}{380}\)

\(8^{12}=\left(8^3\right)^4=512^4\\ 12^8=\left(12^2\right)^4=144^4\\ \)
Nhận thấy: \(512^4>144^4\Rightarrow8^{12}>12^8\)
\(8^{12}=\left(2^3\right)^{12}=2^{36}\)
\(12^8=\left(2^2\cdot3\right)^8=\left(2^2\right)^8\cdot3^8\\ =2^{16}\cdot3^8< 2^{16}\cdot4^8=2^{16}\cdot\left(2^2\right)^8=2^{16}\cdot2^{16}=2^{32}< 2^{36}\)
=> \(12^8< 8^{12}\)


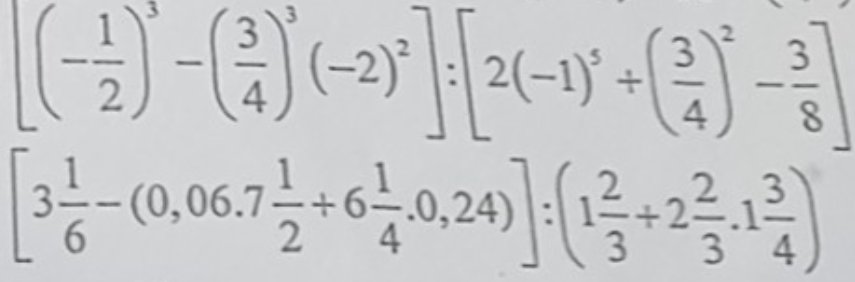
1: A(1;2); C(4;-2)
\(\overrightarrow{AC}=\left(3;-4\right)\)
Phương trình tham số đường thẳng AC là:
\(\left\{{}\begin{matrix}x=1+3t\\y=2-4t\end{matrix}\right.\)
2: \(\overrightarrow{BC}=\left(7;-1\right)\)
=>Vecto pháp tuyến là (1;7)
Phương trình tổng quát của đường thẳng BC là:
1(x+3)+7(y+1)=0
=>x+3+7y+7=0
=>x+7y+10=0
3: M là trung điểm của AB
=>\(\left\{{}\begin{matrix}x_M=\dfrac{1-3}{2}=-1\\y_M=\dfrac{2-1}{2}=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: M(-1;0,5); C(4;-2)
\(\overrightarrow{MC}=\left(5;-2,5\right)=\left(2;-1\right)\)
Phương trình tham số đường thẳng MC là:
\(\left\{{}\begin{matrix}x=4+2t\\y=-2+\left(-1\right)\cdot t=-2-t\end{matrix}\right.\)