Lỗi=#Value

dap an la khong tinh duoc

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED

b: Ta có: ΔBAD=ΔBED

=>BA=BE

Xét ΔBEF vuông tại E và ΔBAC vuông tại A có

BE=BA

\(\widehat{EBF}\) chung

Do đó: ΔBEF=ΔBAC

=>BF=BC

=>ΔBFC cân tại B

a: Sửa đề: Từ B kẻ đường thẳng vuông góc với Oy cắt Ox tại F

Xét ΔOBF vuông tại B và ΔOAE vuông tại A có

OB=OA

\(\widehat{BOF}\) chung

Do đó: ΔOBF=ΔOAE

=>BF=AE

b: Ta có: ΔOBF=ΔOAE

=>OF=OE và \(\widehat{OEA}=\widehat{OFB}\)

Ta có: OA+AF=OF

OB+BE=OE

mà OA=OB và OF=OE

nên AF=BE

Xét ΔIAF vuông tại A và ΔIBE vuông tại B có

AF=BE

\(\widehat{IFA}=\widehat{IEB}\)

Do đó: ΔIAF=ΔIBE

c: Ta có: ΔIAF=ΔIBE

=>IA=IB

Xét ΔOAI vuông tại A và ΔOBI vuông tại B có

OI chung

OA=OB

Do đó: ΔOAI=ΔOBI

=>\(\widehat{AOI}=\widehat{BOI}\)

=>OI là phân giác của góc AOB

Xét ΔMNP có \(\widehat{PMN}=\widehat{PNM}\)

nên ΔPMN cân tại P

Ta có: \(\widehat{PME}=\dfrac{\widehat{PMN}}{2}\)

\(\widehat{PNF}=\dfrac{\widehat{PNM}}{2}\)

mà \(\widehat{PMN}=\widehat{PNM}\)

nên \(\widehat{PME}=\widehat{PNF}\)

Xét ΔPME và ΔPNF có

\(\widehat{PME}=\widehat{PNF}\)

PM=PN

\(\widehat{MPE}\) chung

Do đó: ΔPME=ΔPNF

=>ME=NF

Gọi A là biến cố"Số xuất hiện trên thẻ là số chính phương"

=>A={1;4;9;16;25;36}

=>n(A)=6

=>\(P\left(A\right)=\dfrac{6}{48}=\dfrac{1}{8}\)

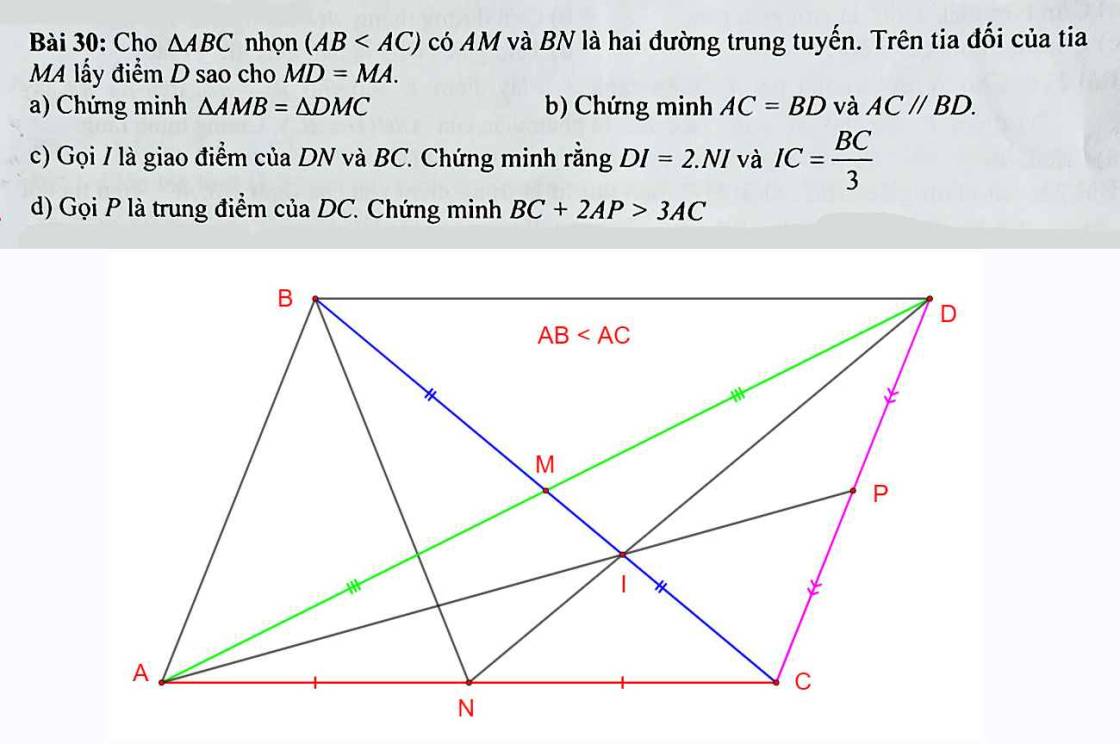
a: Xét ΔAMB và ΔDMC có

MA=MD

\(\widehat{AMB}=\widehat{DMC}\)

MB=MC

Do đó: ΔAMB=ΔDMC

b: Xét ΔMAC và ΔMDB có

MA=MD

\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)

MC=MB

Do đó: ΔMAC=ΔMDB

=>AC=DB

Ta có: ΔMAC=ΔMDB

=>\(\widehat{MAC}=\widehat{MDB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AC//BD

c: Xét ΔADC có

CM,DN là các đường trung tuyến

CM cắt DN tại I

Do đó: I là trọng tâm của ΔADC

Xét ΔADC có

I là trọng tâm của ΔADC

DN là đường trung tuyến và CM là đường trung tuyến

Do đó: DI=2IN và \(CI=\dfrac{2}{3}CM=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{3}\cdot BC\)

a: Ta có: ΔABC vuông tại A

=>\(\widehat{ACB}+\widehat{ABC}=90^0\)

=>\(\widehat{ACB}=90^0-50^0=40^0\)

b: Xét ΔCAD và ΔCED có

CA=CE

\(\widehat{ACD}=\widehat{ECD}\)

CD chung

Do đó: ΔCAD=ΔCED

=>DA=DE
c: Ta có: ΔCAD=ΔCED

=>\(\widehat{CAD}=\widehat{CED}\)

mà \(\widehat{CAD}=90^0\)

nên \(\widehat{CED}=90^0\)

=>DE\(\perp\)CB

Xét ΔDAF vuông tại A và ΔDEB vuông tại E có

DA=DE
\(\widehat{ADF}=\widehat{EDB}\)

Do đó: ΔDAF=ΔDEB

=>DF=DB

=>D nằm trên đường trung trực của BF(1)

Ta có: IF=IB

=>I nằm trên đường trung trực của BF(2)

Ta có: CA+AF=CF
CE+EB=CB

mà CA=CE và AF=EB(ΔDAF=ΔDEB)

nên CF=CB

=>C nằm trên đường trung trực của BF(3)

Từ (1),(2),(3) suy ra C,D,I thẳng hàng

a.

Áp dụng tính chất tổng 3 góc trong tam giác:

\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)

\(\Leftrightarrow50^0+\widehat{ACB}+90^0=180^0\)

\(\Leftrightarrow\widehat{ACB}=40^0\)

b.

Xét hai tam giác DCA và DCE có:

\(\left\{{}\begin{matrix}CA=CE\left(gt\right)\\\widehat{DCA}=\widehat{DCE}\left(\text{CD là phân giác}\right)\\CD\text{ là cạnh chung}\end{matrix}\right.\)

\(\Rightarrow\Delta DCA=\Delta DCE\left(c.g.c\right)\)

\(\Rightarrow DE=DA\)

c.

Từ câu b, do \(\Delta DCA=\Delta DCE\Rightarrow\widehat{DEC}=\widehat{DAC}=90^0\)

Xét hai tam giác CAB và CEF có:

\(\left\{{}\begin{matrix}\widehat{CAB}=\widehat{CEF}=90^0\\CA=CE\left(gt\right)\\\widehat{ACE}-chung\end{matrix}\right.\) \(\Rightarrow\Delta CAB=\Delta CEF\left(g.c.g\right)\)

\(\Rightarrow CB=CF\)

\(\Rightarrow\Delta CBF\) cân tại C

Mà I là trung điểm BF \(\Rightarrow CI\) là trung tuyến nên CI đồng thời là phân giác \(\widehat{ACB}\)

\(\Rightarrow\) Đường thẳng CI trùng đường thẳng AD hay C, D, I thẳng hàng

Phải được thầy, cô giáo tick cho mới được bạn nhé.

Em phải trả lời đúng những câu hỏi đồng thời tùy vào mức độ của đề bài mà các CTV và thầy cô sẽ xem xét chấm điểm cho em nha.