giải giúp em với 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ đường cao BD của tam giác ABC \(\left(D\in AC\right)\)
Khi đó \(AD=AB.cosA=c.cosA\)
\(BD=AB.sinA=c\sqrt{1-cos^2A}\)
\(CD=AC-AD=b-c.cosA\)
Tam giác BCD vuông tại D
\(\Rightarrow BC^2=CD^2+BD^2\)
\(\Leftrightarrow a^2=\left(b-c.cosA\right)^2+\left(c\sqrt{1-cos^2A}\right)^2\)
\(\Leftrightarrow a^2=b^2-2bc.cosA+c^2.cos^2A+c^2\left(1-cos^2A\right)\)
\(\Leftrightarrow a^2=b^2+c^2-2bc.cosA\)
Ta có đpcm.

\(\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+\dfrac{3}{10\cdot13}+...+\dfrac{3}{87\cdot90}\)
\(=\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{87}-\dfrac{1}{90}\)
\(=\dfrac{1}{4}+\left(\dfrac{1}{7}-\dfrac{1}{7}\right)+\left(\dfrac{1}{10}-\dfrac{1}{10}\right)+...+\left(\dfrac{1}{87}-\dfrac{1}{87}\right)-\dfrac{1}{90}\)
\(=\dfrac{1}{4}-\dfrac{1}{90}\)
\(=\dfrac{45}{180}-\dfrac{2}{180}\)
\(=\dfrac{43}{180}\)

1 tạ = 100 kg
a) Số tiền mua cam:
30000 × 100 = 3000000 (đồng)
Số tiền lãi:
3000000 × 15% = 450000 (đồng)
b) Số tiền bán cam nếu cam không bị hư:
40000 × 100 = 4000000 (đồng)
Số tiền bị hao hụt:
4000000 - 3000000 - 450000 = 550000 (đồng)
Số cam bị hỏng:
550000 : 40000 = 13,75 (kg)
a) 1 tạ = 100kg
Số tiền người đó đã bỏ ra là:
\(100\times30000=3000000\left(đ\right)\)
Số tiền lãi là:
\(15\%\times3000000=450000\left(đ\right)\)
b) Người buôn bán hết số cam được số tiền là:
\(3000000+450000=3450000\left(đ\right)\)
Số kg cam người đó đã bán là:
\(3450000:40000=86,25\left(kg\right)\)
Số kg cam bị hỏng là:
\(100-86,25=13,75\left(kg\right)\)

11 × 68 + 46 × 33
= 11 × 68 + 46 × 3 × 11
= 11 × 68 + 132 × 11
= 11 × (68 + 132)
= 11 × 200
= 11 × 2 × 100
= 22 × 100
= 2200
11 x 68 + 46 x 33
=748 + 1518
= 2266
ko biết đúng ko nữa

\(\dfrac{x^2+4+6}{5-6x}< 0\)
Nhận xét:
\(x^2\ge0,\forall x\)
\(\Rightarrow x^2+4+6\ge10,\forall x\)
Do đó \(\dfrac{x^2+4+6}{5-6x}< 0\) khi và chỉ khi:
\(5-6x< 0\)
\(\Leftrightarrow6x>5\)
\(\Leftrightarrow x>\dfrac{5}{6}\)
Vậy \(x>\dfrac{5}{6}\)

\(\sqrt{x}=1-\sqrt{3}\)
Nhận xét:
\(\sqrt{3}>\sqrt{1}=1\)
\(\Rightarrow1-\sqrt{3}< 0\)
\(\Rightarrow\sqrt{x}< 0\) (vô lí)
Vậy không tìm được giá trị x thoả mãn đề bài

\(\left(a+1\right)\left(a+2\right)\left(a+3\right)\left(a+4\right)+1\\ =\left[\left(a+1\right)\left(a+4\right)\right]\left[\left(a+2\right)\left(a+3\right)\right]+1\\ =\left(a^2+5a+4\right)\left(a^2+5a+6\right)+1\\ =\left(a^2+5a+4\right)\left(a^2+5a+4\right)+2\left(a^2+5a+4\right)+1\\ \left(a^2+5a+4\right)^2+2\left(a^2+5a+4\right)+1\\ =\left(a^2+5a+5\right)^2\)

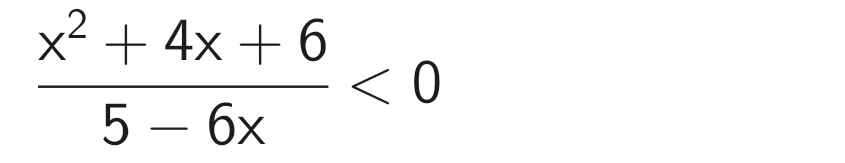
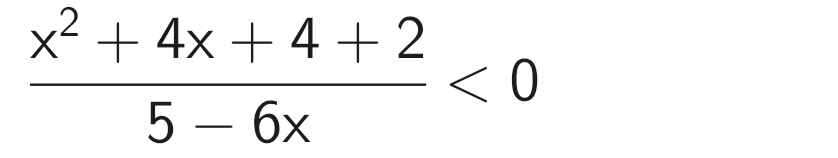
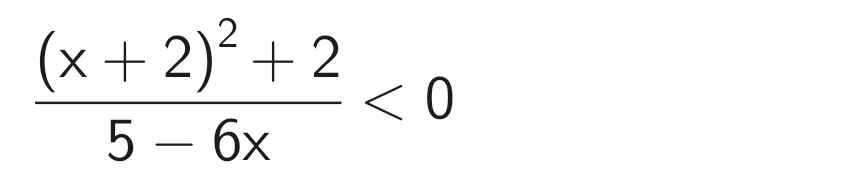

a: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
ΔADB vuông tại D
=>\(DA^2+DB^2=AB^2\)
=>\(DB=\sqrt{5^2-4^2}=3\left(cm\right)\)
b: Xét ΔHDB vuông tại D và ΔHEA vuông tại E có
\(\widehat{DHB}=\widehat{EHA}\)(hai góc đối đỉnh)
Do đó: ΔHDB~ΔHEA
=>\(\dfrac{HD}{HE}=\dfrac{HB}{HA}\)
=>\(HD\cdot HA=HB\cdot HE\)