a: Trên tia AB, ta có: AC<AB

nên C nằm giữa A và B

=>AC+CB=AB

=>CB+1=4

=>CB=3(cm)

b: B là trung điểm của CD

=>\(CD=2\cdot CB=2\cdot3=6\left(cm\right)\)

C là trung điểm của OA

=>\(OC=\dfrac{OA}{2}=4,5\left(cm\right)\)

Trên tia Ox, ta có: OC<OB

nên C nằm giữa O và B

=>OC+CB=OB

=>CB+4,5=12

=>CB=12-4,5=7,5(cm)

Hình bạn tự vẽ nhé.

Ta có: \(ON+NM=OM\\ \Rightarrow3+MN=7\\ \Rightarrow MN=4cm\)

Mà \(A\) là trung điểm \(MN\)

\(\Rightarrow NA=AM=\dfrac{1}{2}MN\\ \Rightarrow NA=AM=2cm\)

Ta có: \(OA=ON+NA\\ \Rightarrow OA=3+2\\ \Rightarrow OA=5cm\)

Vậy...

a) $25.12$

$=25.4.3$

$=100.3=300$

b) $34.99$

$=34.(100-1)$

$=34.100-34.1$

$=3400-34=3366$

c) $47.101$

$=47.(100+1)$

$=47.100+47.1$

$=4700+47=4747$

d) $15.302$

$=15.(300+2)$

$=15.300+15.2$

$=4500+30=4530$

e) $125.32$

$=125.8.4$

$=1000.4=4000$

g) $123.1001$

$=123.(1000+1)$

$=123.1000+123.1$

$=123000+123=123123$

             Đây là toán nâng cao chuyên đề giả thiết tạm, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:

                              Giải:

Giả sử tất cả đều là sọt quýt thì tổng số quả là: 179 x 8 = 1432 (quả)

So với đề bài thì thừa ra là: 1432 - 1120 = 312 (quả)

Cứ thay một sọt quýt bằng một sọt cam thì số quả giảm là:

                  179 - 75 =  104 (quả)

 Số sọt cam là: 312 : 104 = 3 (sọt)

 Số sọt quýt là: 8 -  3  = 5 (sọt)

 Số cam là: 75 x 3 =  225 (quả)

  Số quýt là: 179 x 5  = 895 (quả)

 Đáp số:....

Bạn tự vẽ hình nhé

Ta có E là trung điểm MN (gt)

\(\Rightarrow EM=EN=\dfrac{1}{2}MN\\ \Rightarrow EM=EN=6cm\)

Mà \(F\) là trung điểm \(EN\)

\(\RightarrowÈF=FN=\dfrac{1}{2}EN\\ \RightarrowÈ=FN=3cm\) 

Vậy...

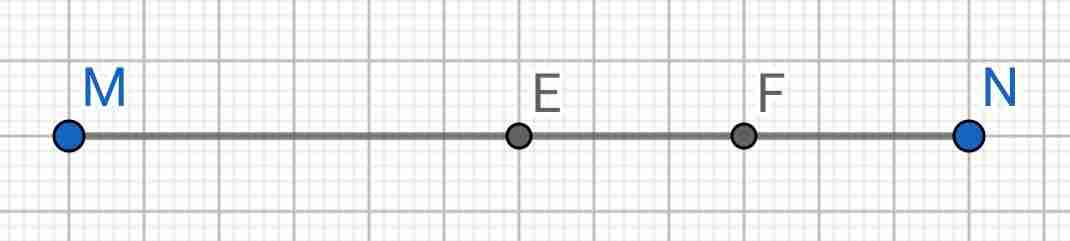
Do E là trung điểm của MN

=> NE = MN : 2

= 12 : 2

= 6 (cm)

Do F là trung điểm của NE

=> EF = NE : 2

= 6 : 2

= 3 (cm)

Số các số hạng:

   \(\left(99-1\right):2+1=50\) ( số )

Tổng dãy số trên:

     \(\dfrac{\left(99+1\right)\times50}{2}=2500\)

Số số hạng:
(99 - 1) : 2 + 1 = 50 (số)
Tổng là:
(99 + 1) × 50 : 2 = 2500

sai đề rồi

Dựa vào đồ thị, ta thấy \(m=\min\limits_{\left[-1;3\right]}f\left(x\right)=f\left(2\right)=-4\)

và \(M=\max\limits_{\left[-1;3\right]}f\left(x\right)=f\left(-1\right)=2\)

Khi đó \(M+m=2-4=-2\)