Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: -526,8<0
0<0,65
Do đó: -526,8<0,65
b: 6,45>0
0>-3,273
Do đó 6,45>-3,273
c: 7,78<9,56
=>-7,78>-9,56
d: 0,789>0,356
=>-0,789<-0,356

\(P\left(1\right)=1^3-2\cdot a\cdot1+a^2=a^2-2a+1\)
\(Q\left(3\right)=3^2+\left(3a+1\right)\cdot3+a^2=a^2+9a+12\)
P(1)=Q(3)
=>\(a^2+9a+12=a^2-2a+1\)
=>11a=-11
=>a=-1

x+y-3=0
=>x+y=3
\(M\left(x\right)=x^3+x^2y-3x^2-xy-y^2+4y+x+2020\)
\(=x^2\left(x+y\right)-3x^2-y\left(x+y\right)+4y+x+2020\)
\(=3x^2-3x^2-3y+4y+x+2020\)
=x+y+2020
=3+2020
=2023

\(\dfrac{Hàng\text{ }ngàn\text{ }cây}{Chủ\text{ }ngữ}\dfrac{xanh}{Vị\text{ }ngữ}\)

a) \(P\left(x\right)=x^5-2x^4+3x^2-x+2;Q\left(x\right)=x^4-2x^3+x-5\)
+, \(P\left(x\right)+Q\left(x\right)=\left(x^5-2x^4+3x^2-x+2\right)+\left(x^4-2x^3+x-5\right)\)
\(=x^5-2x^4+3x^2-x+2+x^4-2x^3+x-5\)
\(=x^5+\left(-2x^4+x^4\right)-2x^3+3x^2+\left(-x+x\right)+\left(2-5\right)\)
\(=x^5-x^4-2x^3+3x^2-3\)
+, \(P\left(x\right)-Q\left(x\right)=\left(x^5-2x^4+3x^2-x+2\right)-\left(x^4-2x^3+x-5\right)\)
\(=x^5-2x^4+3x^2-x+2-x^4+2x^3-x+5\)
\(=x^5+\left(-2x^4-x^4\right)+2x^3+3x^2+\left(-x-x\right)+\left(2+5\right)\)
\(=x^5-3x^4+2x^3+3x^2-2x+7\)
b) \(P\left(x\right)=x^4+3x^5-x^2-4;Q\left(x\right)=x^4-x^2-3x^3+x\)
+, \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^5-x^2-4\right)+\left(x^4-x^2-3x^3+x\right)\)
\(=x^4+3x^5-x^2-4+x^4-x^2-3x^3+x\)
\(=3x^5+\left(x^4+x^4\right)-3x^3+\left(-x^2-x^2\right)+x-4\)
\(=3x^5+2x^4-3x^3-2x^2+x-4\)
+, \(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^5-x^2-4\right)-\left(x^4-x^2-3x^3+x\right)\)
\(=x^4+3x^5-x^2-4-x^4+x^2+3x^3-x\)
\(=3x^5+\left(x^4-x^4\right)+3x^3+\left(-x^2+x^2\right)-x-4\)
\(=3x^5+3x^3-x-4\)
\(\text{#}Toru\)



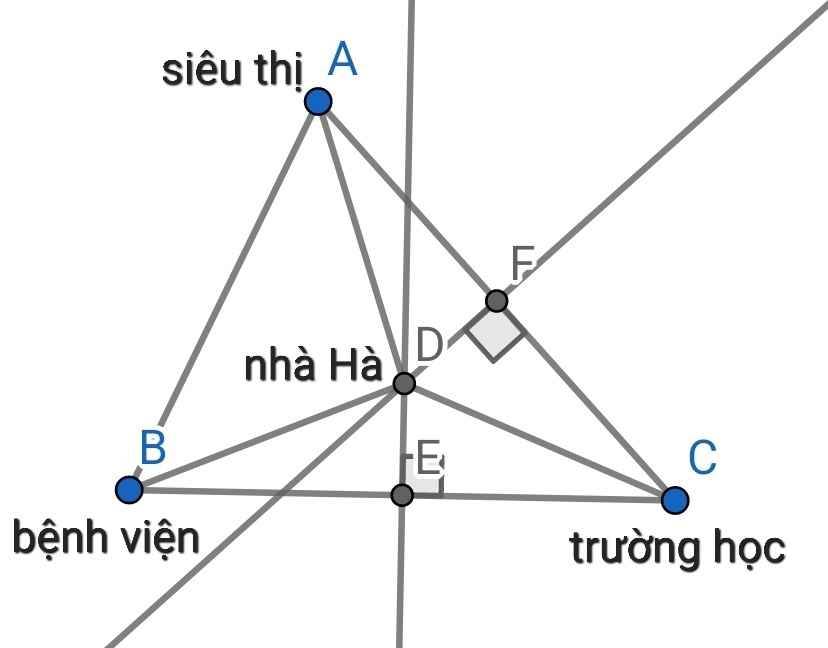
Để khoảng cách từ vị trí của nhà Hà đến siêu thị, bệnh viện, trường học đều bằng nhau thì nhà Hà nằm ở vị trí D là giao điểm của ba đường trung trực của ∆ABC như hình vẽ.
Siêu thị, bệnh viện, trường học nằm ở ba vị trí là ba đỉnh của ∆ABC

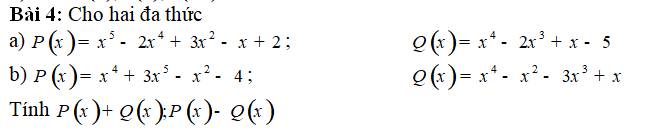

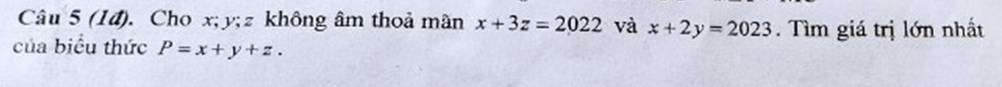
\(\dfrac{x^5+5x^3-3x^4-2x^2+3x-6}{x^2-3x+5}\)
\(=\dfrac{x^5-3x^4+5x^3-2x^2+6x-10-3x+4}{x^2-3x+5}\)
\(=\dfrac{x^3\left(x^2-3x+5\right)-2\left(x^2-3x+5\right)-3x+4}{x^2-3x+5}\)
\(=x^3-2+\dfrac{-3x+4}{x^2-3x+5}\)