cho\(\dfrac{7x+5y}{3x-7y}=\dfrac{7z+5t}{3z-5t}\).CMR \(\dfrac{x}{y}=\dfrac{z}{t}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(C=A-B=x^2-5xy+5y^2-3x+18y-\left(-x^2+3xy-y^2-x-7\right)\\ =x^2-5xy+5y^2-3x+18y+x^2-3xy+y^2+x+7\\ =\left(x^2+x^2\right)+\left(-5xy-3xy\right)+\left(5y^2+y^2\right)+\left(-3x+x\right)+18y+7\)
\(=2x^2-8xy+6y^2-2x+18y+7\)
Bạn xem lại đề nhé, mình nghĩ không tính được giá trị C khi x-y=4 nhé.

-3/4 . -8/9 . ... . -4084440/4084440
= 3/4 . 8/9 . 4084440/4084441
=1.3/2.2 . 2.4/3.3 ... 2020.2022/2021.2021
=1.3.2.4...2020.2022/2.2.3.3...2021.2021
=(1.2...2020)(3.4...2022)/(2.3...2021)(2.3...2021)
=1.2022/2021.2=2022/4042

Nhớ hóng những câu hỏi hay của cô thương hoài để có thưởng nha
Mình thích cô thương hoài lắm lun, hóng câu hỏi của cô cũng đc quà và cô chuyên nghiệp, nhiệt tình lắm đó nha

Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x-2020|+|x-2024|=|x-2020|+|2024-x|\geq |x-2020+2024-x|=4$
$|x-2022|\geq 0$ (theo tính chất trị tuyệt đối)
$\Rightarrow |x-2020|+|x-2024|+|x-2022|\geq 4+0=4$
$\Rightarrow P\geq 4$
Vậy $P_{\min}=4$. Giá trị này đạt được khi $(x-2020)(2024-x)\geq 0$ và $x-2022=0$
Hay $x=2022$

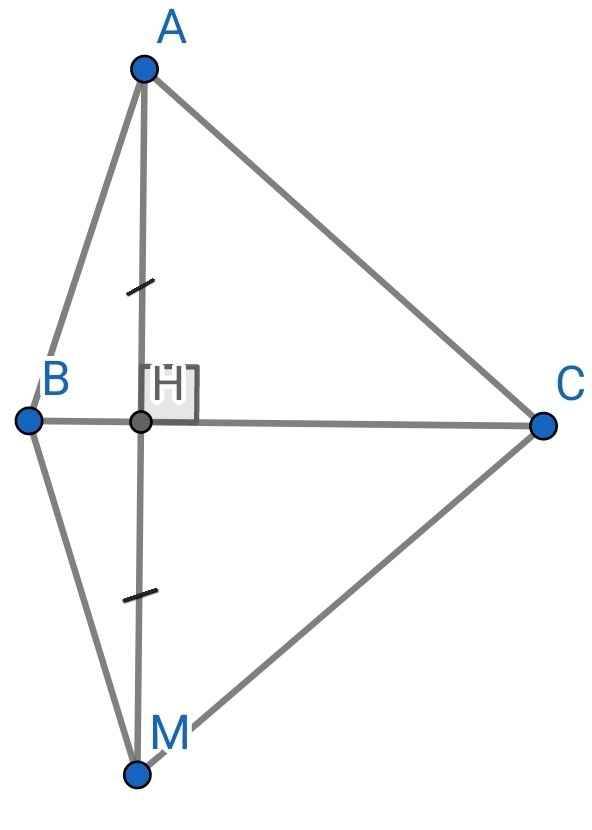 a) Xét hai tam giác vuông: ∆AHC và ∆MHC có:
a) Xét hai tam giác vuông: ∆AHC và ∆MHC có:
HC là cạnh ccung
AH = MH (gt)
⇒ ∆AHC = ∆MHC (hai cạnh góc vuông)
b) Do ∆AHC = ∆MHC (cmt)
⇒ ∠ACH = ∠MCH (hai góc tương ứng)
AC = MC (hai cạnh tương ứng)
Do ∠ACH = ∠MCH (cmt)
⇒ ∠ACB = ∠MCB
Xét ∆ABC và ∆MBC có:
AC = MC (cmt)
∠ACB = ∠MCB (cmt)
BC là cạnh chung
⇒ ∆ABC = ∆MBC (c-g-c)
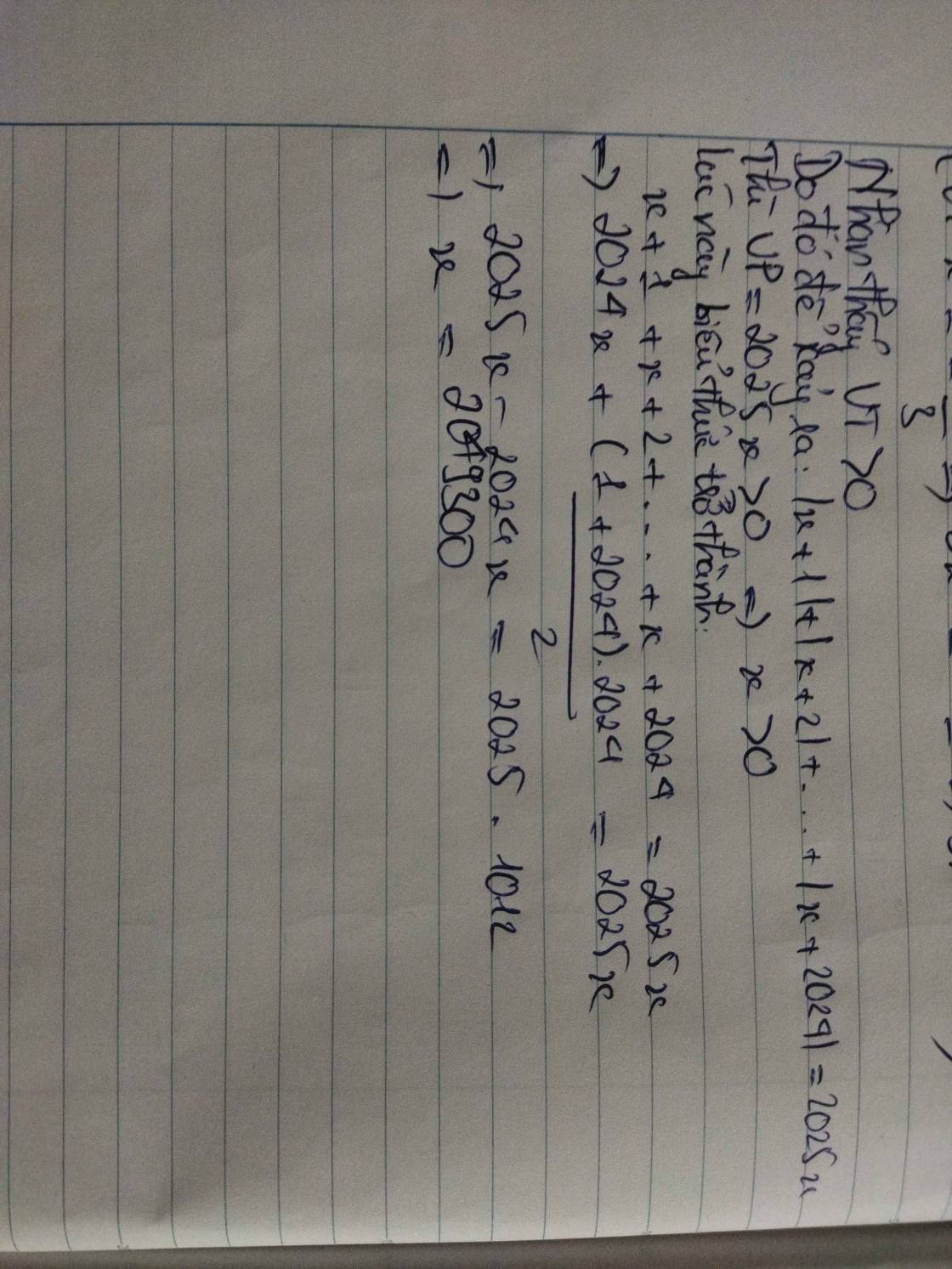
Lời giải:
$\frac{7x+5y}{3x-5y}=\frac{7z+5t}{3z-5t}$
$\Rightarrow (7x+5y)(3z-5t)=(7z+5t)(3x-5y)$
$\Rightarrow 21xz-35xt+15yz-25yt = 21xz-35yz+15xt-25yt$
$\Rightarrow -35xt+15yz=-35yz+15xt$
$\Rightarrow -50xt=-50yz$
$\Rightarrow xt=yz\Rightarrow \frac{x}{y}=\frac{z}{t}$