A(x)=(7x²-5x²-2x²)-(6x³-10x³)+2x-12

A(x)=-4x³+2x-12

Sắp xếp:-4x³+2x-12

\(A\left(x\right)=\left(7x^2-5x^2-2x^2\right)-\left(6x^3-10x^3\right)+2x-12\)

\(A\left(x\right)=-4x^3+2x-12\)

Sắp xếp:\(-4x^3+2x-12\)

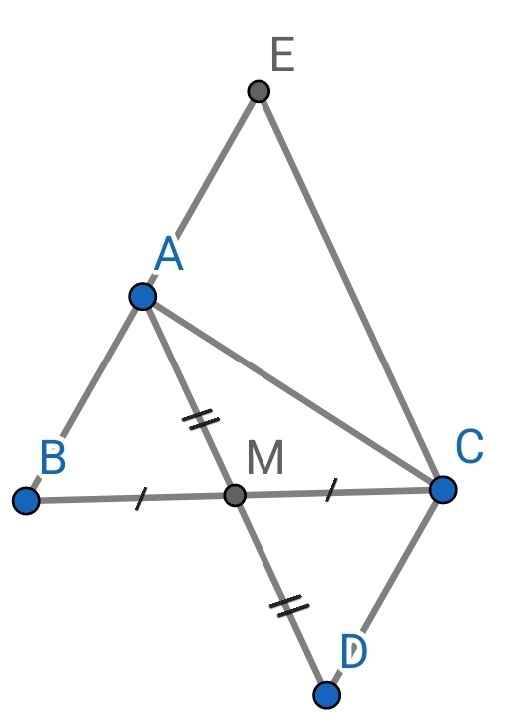 a) Do M là trung điểm của BC (gt)

⇒ BM = MC

Do M là trung điểm của AD (gt)

⇒ AM = MD

Xét ∆ABM và ∆DCM có:

AM = MD (cmt)

∠AMB = ∠CMD (đối đỉnh)

BM = MC (cmt)

⇒ ∆ABM = ∆DCM (c-g-c)

b) Do ∆ABM = ∆DCM (cmt)

⇒ ∠ABM = ∠CDM (hai góc tương ứng)

Mà ∠ABM và ∠CDM là hai góc so le trong

⇒ AB // CD

c) Do AB // CD (cmt)

⇒ ∠CAE = ∠ACD (so le trong)

∠ACE = ∠CAD (so le trong)

Xét ∆ACE và ∆CAD có:

∠ACE = ∠CAD (cmt)

AC là cạnh chung

∠CAE = ∠ACD (cmt)

⇒ ∆ACE = ∆CAD (g-c-g)

⇒ AE = CD (hai cạnh tương ứng)

Do ∆ABM = ∆DCM (cmt)

⇒ AB = CD (hai cạnh tương ứng)

Mà AE = CD (cmt)

⇒ AB = AE

Vậy A là trung điểm của BE

là học sinh giỏi

là học sinh giỏi bạn ạ

- \(\dfrac{2}{y}\) = \(\dfrac{y}{-32}\)

-2.(-32) = y.y

y² = 64

\(\left[{}\begin{matrix}y=-8\\y=8\end{matrix}\right.\)

y \(\in\) {-8; 8}

-2/y = y/(-32)

y.y = (-2).(-32)

y² = 64

⇒ y = -8 hoặc y = 8

:))

???

???

\(M=\left|x-22\right|+\left|x+12\right|\)

\(M=\left|22-x\right|+\left|x+12\right|\ge\left|22-x+x+12\right|\)

\(M=\left|22-x\right|+\left|x+12\right|\ge34\)

\(M\ge34\)

Dấu "\(=\)" xảy ra khi:

\(\left(22-x\right)\left(x+12\right)\ge0\)

\(TH1:22-x\ge0;x+12\ge0\)

\(\Rightarrow22\ge x\ge-12\)

\(TH2:22-x\le0;x+12\ge0\)

\(\Rightarrow22\le x;x\ge12\left(vô.lý\right)\)

Vậy \(GTNN\) của \(M\) là \(34\) khi \(22\ge x\ge-12\)

Lời giải:
a. Xét tam giác $AMB$ à $AMC$ có:

$AB=AC$ (do tam giác $ABC$ cân tại $A$)

$MB=MC$ (do $M$ là trung điểm $BC$

$AM$ chung

$\Rightarrow \triangle AMB=\triangle AMC$ (c.c.c)

b. 

Từ tam giác bằng nhau phần a

$\Rightarrow \widehat{BAM}=\widehat{CAM}$ 

$\Rightarrow AM$ là phân giác $\widehat{BAC}$

c.

Xét tam giác $ABM$ và $DCM$ có:

$BM=CM$

$AM=DM$ (gt)

$\widehat{AMB}=\widehat{DMC}$ (đối đỉnh) 

$\Rightarrow \triangle ABM=\triangle DCM$ (c.g.c)

$\Rightarrow \widehat{BAM}=\widehat{CDM}$

Mà 2 góc này ở vị trí so le trong nên $AB\parallel CD$

Hình vẽ:

a) \(1,2-3^2+7,5:3\)

\(=1,2-9+2,5\)

\(=-7,8+2,5=-5,3\)

b) \(\dfrac{9^{11}\cdot25^6}{15^6\cdot27^5}=\dfrac{\left(3^2\right)^{11}\cdot\left(5^2\right)^6}{\left(3\cdot5\right)^6\cdot\left(3^3\right)^5}=\dfrac{3^{22}\cdot5^{12}}{3^6\cdot5^6\cdot3^{15}}\)

\(=\dfrac{3^{22}\cdot5^{12}}{3^{21}\cdot5^6}=3\cdot5^6=46875\)

c) \(\left|\dfrac{3}{8}-\dfrac{9}{16}\right|-\sqrt{\dfrac{25}{64}}+\left(\dfrac{7}{16}\right)^5:\left(\dfrac{7}{16}\right)^4\)

\(=\left|\dfrac{6}{16}-\dfrac{9}{16}\right|-\sqrt{\dfrac{5^2}{8^2}}+\dfrac{7}{16}\)

\(=\left|-\dfrac{3}{16}\right|-\sqrt{\left(\dfrac{5}{8}\right)^2}+\dfrac{7}{16}\)

\(=\dfrac{3}{16}-\dfrac{5}{8}+\dfrac{7}{16}\)

\(=\dfrac{3}{16}-\dfrac{10}{16}+\dfrac{7}{16}\)

\(=\dfrac{3-10+7}{16}=0\)

d) \(\sqrt{\left(\dfrac{-1}{4}\right)^2}-3.\sqrt{\dfrac{25}{81}}+\left|\dfrac{7}{4}-\dfrac{1}{3}\right|\)

\(=\left|\dfrac{-1}{4}\right|-3.\sqrt{\left(\dfrac{5}{9}\right)^2}+\left|\dfrac{17}{12}\right|\\ =\dfrac{1}{4}-3.\left|\dfrac{5}{9}\right|+\dfrac{17}{12}\\ =\dfrac{1}{4}-3.\dfrac{5}{9}+\dfrac{17}{12}\\ =\dfrac{1}{4}-\dfrac{15}{9}+\dfrac{17}{12}\\ =-\dfrac{17}{12}+\dfrac{17}{12}=0\)

\(A=\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\)

\(3A=1+\dfrac{2}{3}+\dfrac{3}{3^2}+...+\dfrac{100}{3^{99}}\)

\(\Rightarrow3A-A=1+\dfrac{2}{3}-\dfrac{1}{3}+\dfrac{3}{3^2}-\dfrac{2}{3^2}+\dfrac{4}{3^3}-\dfrac{3}{3^3}+...+\dfrac{100}{3^{99}}-\dfrac{99}{3^{99}}-\dfrac{100}{3^{100}}\)

\(\Rightarrow2A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\)

\(\Rightarrow6A=3+1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\)

\(\Rightarrow6A-2A=3-\dfrac{101}{3^{99}}+\dfrac{100}{3^{100}}\)

\(\Rightarrow4A=3-\dfrac{203}{3^{100}}< 3\)

\(\Rightarrow A< \dfrac{3}{4}\)

\(A< \dfrac{3}{4}\)

Vẫn tuỳ thuộc vào điểm TBM cả năm em nhé