(x-2)^2-x|x-2|=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\widehat{B}=x;\widehat{C}=y\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(x+y=180^0-60^0=120^0\)
Vì góc B và góc C tỉ lệ nghịch với 5 và 3
=>5x=3y
=>\(\dfrac{x}{3}=\dfrac{y}{5}\)
mà x+y=120
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{120}{8}=15\)
=>\(x=15\cdot3=45^0;y=5\cdot15=75^0\)
vậy: \(\widehat{B}=45^0;\widehat{C}=75^0\)

Bài 1:
a. Do $a,b$ tỉ lệ thuận với nhau nên với $k$ là hệ số tỉ lệ của $a$ đối với $b$ thì:
$a=bk$
Thay $a=2, b=18$ thì: $2=18k\Rightarrow k=\frac{1}{9}$
b. Khi $a=5$ thì: $a=bk$
$\Rightarrow 5=\frac{1}{9}b\Rightarrow b=45$
Bài 2:
a. Gọi $k$ là hệ số tỉ lệ của $y$ đối với $x$ thì:
$y=kx$
Thay $x=7; y=21$ thì: $21=7k\Rightarrow k=3$
Vậy $y=3x$
b. Gọi $m$ là hệ số tỉ lệ của $x$ đối với $y$ thì: $x=my$
Thay $x=7; y=21$ thì: $7=21m\Rightarrow m=\frac{1}{3}$
Vậy $x=\frac{1}{3}y$

Gọi số hàng của đội hai lần lượt là: \(x;y\) (tấn); đk \(x;y\in\) Z+
Theo bài ra ta có: \(\dfrac{x}{13}\) = \(\dfrac{y}{16}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{13}=\dfrac{y}{16}=\dfrac{y-x}{16-13}\) = \(\dfrac{36}{3}\) = 12
\(x\) = 12 x 13 =156
y = 12 x 16 = 192
Kết luận:..

Số bi xanh bằng: 1 : \(\dfrac{6}{7}\) = \(\dfrac{7}{6}\) (bi vàng)
92 viên bi ứng với phân số là:
\(\dfrac{5}{3}\) + 1 + \(\dfrac{7}{6}\) = \(\dfrac{23}{6}\) (bi vàng)
Số bi vàng là:
92 : \(\dfrac{23}{6}\) = 24 (viên bi)
Số bi xanh là: 24 x \(\dfrac{7}{6}\) = 28 (viên bi)
Số bi đỏ là: 24 x \(\dfrac{5}{3}\) = 40 (viên bi)
Kết luận:..
\(\dfrac{\text{Số bi đỏ }}{\text{Số bi vàng }}=\dfrac{5}{3}\)
=> \(\dfrac{\text{Số bi vàng}}{\text{Số bi đỏ }}=\dfrac{3}{5}\)
\(\dfrac{\text{Số bi vàng }}{\text{Số bi xanh }}=\dfrac{6}{7}\)
Để cho cùng tử (bi vàng) thì ta quy đồng:
\(\dfrac{\text{Số bi vàng}}{\text{Số bi đỏ }}=\dfrac{3}{5}=\dfrac{6}{10}\)
Vậy ta có sơ đồ:
Số bi vàng: |----|----|----|----|----|----|
Số bi đỏ : |----|----|----|----|----|----|----|----|----|----|
Số bi xanh: |----|----|----|----|----|----|----|
Tổng số phần bằng nhau là:
6+10+7=23 (phần)
Giá trị 1 phần là:
92 : 23 = 4 (viên bi)
=> Số bi vàng là:
4 x 6 = 24 (viên)
Số bi đỏ là:
4 x 10 = 40 (viên)
Số bi xanh là:
4 x 7 = 28 (viên)
Đ/S:...
(Cho GP ạ)
> \(\dfrac{\text{Số bi vàng}}{\text{Số bi đỏ }}=\dfrac{3}{5}\)
\(\dfrac{\text{Số bi vàng }}{\text{Số bi xanh }}=\dfrac{6}{7}\)
Để cho cùng tử (bi vàng) thì ta quy đồng:
\(\dfrac{\text{Số bi vàng}}{\text{Số bi đỏ }}=\dfrac{3}{5}=\dfrac{6}{10}\)
Vậy ta có sơ đồ:
Số bi vàng: |----|----|----|----|----|----|
Số bi đỏ : |----|----|----|----|----|----|----|----|----|----|
Số bi xanh: |----|----|----|----|----|----|----|
Tổng số phần bằng nhau là:
6+10+7=23 (phần)
Giá trị 1 phần là:
92 : 23 = 4 (viên bi)
=> Số bi vàng là:
4 x 6 = 24 (viên)
Số bi đỏ là:
4 x 10 = 40 (viên)
Số bi xanh là:
4 x 7 = 28 (viên)
Đ/S:...
(Cho GP ạ)

C = 2024 - | 2022\(x\) - 1|
Vì |2022\(x\) - 1| ≥ 0
- |2022\(x\) - 1| ≤ 0
C = 2024 - |2022\(x\) - 1| ≤ 2024
Cmax = 2024 xảy ra khi \(x=\dfrac{1}{2022}\)
Vậy biểu thức không có giá trị nhỏ nhất.

\(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Rightarrow\dfrac{a}{b}+1=\dfrac{c}{d}+1\)
\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{b}=\dfrac{c}{d}+\dfrac{d}{d}\)
\(\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
Ta có đpcm.
Vì \(\dfrac{a}{b}=\dfrac{c}{d}\) nên ta thấy khi rút gọn 1 phân số thì cả tử số và mẫu số của 2 phân số đều giống nhau.
⇒a=c; b=d
Vì \(a=c;b=d\) nên ta có \(\dfrac{a+b}{b}=\dfrac{c+d}{d}\).
Theo ý kiến của mình là vậy ạ.

Nhà thông thái đem đến 1 con ngựa
Lúc này : 17+1=18 con
Người con cả có: 18:2=9 con
Người con thứ 2 có : 18:3=6 con
Người con thứ 3 có : 18:9=2 con
mà 9+6+2=17 con ( đúng với dữ liệu ban đầu)
Trả lại cho nhà thông thái 1 con mượn lúc đầu
Vậy đã chia được bò cho 3 anh em
K bt có đúng k

a) x và y là hai đại lượng tỉ lệ nghịch theo hệ số a nên:
`a=y/x=4/2=2`
b) Ta có: `a=2`
`=>y/x=2=>y=2x`
c) khi `y=-1=>2x=-1=>x=-1/2`
Khi `y=2=>2x=2=>x=1`
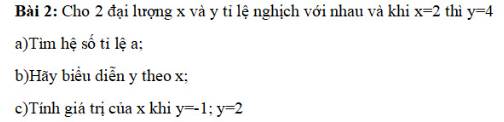
(\(x-2\))2 - \(x\).|\(x-2\)| = 0
(\(x-2\))2 = \(x.\left|x-2\right|\) (đk \(x\) > 0)
(\(x-2\))2 = (\(x\)\(.\left|x-2\right|\))2
(\(x-2\))2 = \(x^2\).(\(x-2\))2
(\(x-2\))2 - \(x^2\).(\(x-2\))2 = 0
(\(x-2\))2.(1 - \(x^2\)) = 0
\(\left[{}\begin{matrix}\left(x-2\right)^2=0\\1-x^2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=2\\x=-1\\x=1\end{matrix}\right.\)
Vì \(x>0\)Vậy \(x\) \(\in\) {1; 2}