Tìm a để 246a là số lớn nhất có bốn chữ số chia hết cho 2và3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Diện tích tam giác BAC là:
\(S_{BAC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC=\dfrac{1}{2}\cdot5,2\cdot3,5\cdot sin75=\dfrac{91\sqrt{6}+91\sqrt{2}}{40}\)
ABCD là hình bình hành
=>\(S_{ABCD}=2\cdot S_{BAC}=\dfrac{91\sqrt{6}+91\sqrt{2}}{20}\)

\(8-x>\dfrac{11}{3}\)
=>\(-x>\dfrac{11}{3}-8=-\dfrac{13}{3}\)
=>\(x< \dfrac{13}{3}\)
mà x là số tự nhiên lớn nhất có thể
nên x=4
8 - \(x\) > \(\dfrac{11}{3}\)
suy ra 8 - \(\dfrac{11}{3}\) > \(x\)
\(\dfrac{24}{3}\) - \(\dfrac{11}{3}\) > \(x\)
\(\dfrac{13}{3}\) > \(x\)
4\(\dfrac{1}{3}\) > \(x\)
Vậy \(x\) = 0; 1; 2; 3; 4
Vì \(x\) là số tự nhiên lớn nhất nên \(x\) = 4

\(x^2+2>=2\forall x\)
=>\(\left(x^2+2\right)^2>=4\forall x\)
=>\(-\left(x^2+2\right)^2< =-4\forall x\)
mà \(-\left(y^2-16\right)^4< =0\forall y\)
nên \(-\left(x^2+2\right)^2-\left(y^2-16\right)^4< =-4\forall x,y\)
=>\(B=-\left(x^2+2\right)^2-\left(y^2-16\right)^4+20< =-4+20=16\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=0\\y^2-16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y\in\left\{4;-4\right\}\end{matrix}\right.\)

ABCD là hình chữ nhật
=> CD = AB = 4 (cm)
=> AD = BC = 3 (cm)
=> BD = AC = 5 (cm)

Số sách đủ để chia là:
\(3+3=6\left(quyển\right)\)
Tổ được chia 8 quyển nhiều hơn tổ được chia 7 quyển là:
\(8-7=1\left(quyển\right)\)
Số tổ được chia sách là:
\(6:1=6\left(tổ\right)\)
Số sách văn và toán là:
\(7\times6+3=45\left(quyển\right)\) Đ/S:...
Ta có:
\(Q=\dfrac{1}{x^2-4x+11}=\dfrac{1}{\left(x^2-4x+4\right)+7}\\ =\dfrac{1}{\left(x-2\cdot x\cdot2+2^2\right)+7}=\dfrac{1}{\left(x-2\right)^2+7}\)
\(\left(x-2\right)^2\ge0\forall x=>\left(x-2\right)^2+7\ge7\forall x\\ =>Q=\dfrac{1}{\left(x-2\right)^2+7}\le\dfrac{1}{7}\forall x\)
Dấu "=" xảy ra: `x-2=0<=>x=2`

1) 12 ⋮ x => x ∈ Ư(12) = {1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 12; -12}
Mà: x > 2
=> x ∈ {3; 4; 6; 12}
2) 24 ⋮ x => x ∈ Ư(24) = {1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 8; -8; 12; -12; 24; -24}
Mà: x > 4
=> x ∈ {6; 8; 12; 24}
3) 36 ⋮ x => x ∈ Ư(36) = {1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 9; -9; 12; -12; 18; -18; 36; -36}
Mà: x ≥ 3
=> x ∈ {3; 4; 6; 9; 12; 18; 36}
4) 40 ⋮ x => x ∈ Ư(40) = {1; -1; 2; -2; 4; -4; 5; -5; 8; -8; 10; -10; 20; -20; 40; -40}
Mà: x < 10 và x là số tự nhiên
=> x ∈ {1; 2; 4; 8}

\(10x-x^2+2\\
=\left(-x^2+10x-25\right)+27\\
=-\left(x^2-10x+25\right)+27\\
=-\left(x-5\right)^2+27\)
Ta có: \(-\left(x-5\right)^2\le0\forall x=>-\left(x-5\right)^2+27\le27\forall x\)
Dấu "=" xảy ra: `x-5=0<=>x=5`

Bài 1:
A = 8.(32 + 1)(34 + 1)(38 + 1)(316 + 1)
A = (32 - 1)(32 + 1)(34+ 1)(38 +1)(316 + 1)
A = (34 - 1)(34 + 1)(38+ 1)(316 + 1)
A = (38 - 1)(38 + 1)(316 + 1)
A = (316 - 1)(316 +1)
A = (316)2 - 12
A = 332 - 1
1: \(A=8\left(3^2+1\right)\left(3^4+1\right)\cdot...\cdot\left(3^{16}+1\right)\)
\(=\left(3^2-1\right)\left(3^2+1\right)\cdot\left(3^4+1\right)\left(3^8+1\right)\cdot\left(3^{16}+1\right)\)
\(=\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=\left(3^8-1\right)\cdot\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=\left(3^{16}-1\right)\left(3^{16}+1\right)=3^{32}-1\)
2: \(B=\left(1-3\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=-\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=-\left(3^4-1\right)\left(3^4+1\right)\cdot\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=-\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)=-\left(3^{16}-1\right)\left(3^{16}+1\right)\)
\(=-\left(3^{32}-1\right)=1-3^{32}\)
3: \(C=24\left(5^2+1\right)\left(5^4+1\right)\cdot...\cdot\left(5^{128}+1\right)+\left(5^{256}-1\right)\)
\(=\left(5^2-1\right)\left(5^2+1\right)\cdot\left(5^4+1\right)\left(5^{128}+1\right)+\left(5^{256}-1\right)\)
\(=\left(5^4-1\right)\cdot\left(5^4+1\right)\cdot...\cdot\left(5^{128}+1\right)+\left(5^{256}-1\right)\)
\(=\left(5^8-1\right)\left(5^8+1\right)\cdot...\cdot\left(5^{128}+1\right)+\left(5^{256}-1\right)\)
\(=\left(5^{16}-1\right)\left(5^{16}+1\right)\cdot...\cdot\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^{32}-1\right)\left(5^{32}+1\right)\left(5^{64}+1\right)\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^{64}-1\right)\left(5^{64}+1\right)\left(5^{128}+1\right)+5^{256}-1\)
\(=\left(5^{128}-1\right)\left(5^{128}+1\right)+5^{256}-1=2\left(5^{256}-1\right)\)
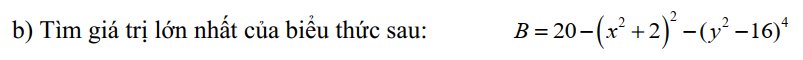
+) 246a chia hết cho 2
=> a ∈ {0; 2; 4; 6; 8} (1)
+) 246a chia hết cho 3
=> 2 + 4 + 6 + a = 12 + a chia hết cho 3
12 ⋮ 3 => a ⋮ 3 => a ∈ {0; 3; 6; 9} (2)
Từ (1) và (2) => a = 0 hoặc a = 6
Để 246a là số lớn nhất thì a = 6 (vì 2460 < 2466)