Ta có a: 6 dư 5
=> a= 6k+5 với k ϵ N
có: a² = (6k+5)² = 36k²+ 60k+25
vì 36k²⋮6 ; 60k⋮6 ; 25 : 6 dư 1
=> a² chia 6 dư 1 
 

Lời giải:

Vì $a$ chia $6$ dư $5$ nên đặt $a=6k+5$ với $k$ nguyên. 

Khi đó: $a^2=(6k+5)^2=36k^2+25+60k=6(6k^2+10k+4)+1$ chia $6$ dư $1$

\((x-y+2)^2\\=x^2+y^2+2^2-2xy-2\cdot y\cdot2+2\cdot x\cdot2\\=x^2+y^2+4-2xy-4y+4x\)

\(\dfrac{4x+2}{4x-2}+\dfrac{3-6x}{6x-6}\left(dkxd:x\ne\dfrac{1}{2};x\ne1\right)\)

\(=\dfrac{2\left(2x+1\right)}{2\left(2x-1\right)}+\dfrac{3\left(1-2x\right)}{6\left(x-1\right)}\)

\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2\left(x-1\right)}\)

\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2x-2}\)

\(=\dfrac{\left(2x+1\right)\left(2x-2\right)}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{\left(1-2x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{4x^2-2x-2}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{4x^2-2x-2-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{2x-3}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{2x-3}{4x^2-6x+2}\)

\(x\) + 2y = 8

\(2y\)        = 8 - \(x\)

 y        = \(\dfrac{8-x}{2}\)

  y =  - \(\dfrac{x}{2}\) + 4

Thay y = - \(\dfrac{x}{2}\) + 4 vào biểu thức B = \(xy\) ta có: 

B = \(x\).(-\(\dfrac{x}{2}\) + 4)

B = - \(\dfrac{x^2}{2}\) + 4\(x\)

B = -\(\dfrac{1}{2}\). (\(x^2\)  - 8\(x\)  + 16)  +  8 

B = - \(\dfrac{1}{2}\).(\(x\) - 4)² + 8

Vì  \(\dfrac{1}{2}\).(\(x\) - 4)² ≥ 0 ⇒ - \(\dfrac{1}{2}\).(\(x\) - 4)² ≤ 0 ⇒ - \(\dfrac{1}{2}\).(\(x\)  - 4)² + 8 ≤ 8

Dấu bằng xảy ra khi:  \(x\) - 4 = 0 ⇒ \(x\) = 4; thay \(x\) = 4 vào biểu thức:

y = - \(\dfrac{1}{2}\) \(x\)+ 4 ta có y = - \(\dfrac{4}{2}\) + 4 = 2

Vậy giá trị lớn nhất của B là 8 xảy ra khi \(x\) = 4; y = 2

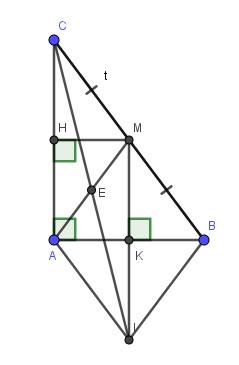
a) Do \(MH\perp AC\left(gt\right)\)

\(\Rightarrow\widehat{MHA}=90^0\)

Do \(MK\perp AB\left(gt\right)\)

\(\Rightarrow\widehat{MKA}=90^0\)

Do \(\Delta ABC\) vuông tại A

\(\Rightarrow\widehat{CAB}=90^0\)

\(\Rightarrow\widehat{HAK}=90^0\)

Tứ giác \(AKMH\) có:

\(\widehat{MHA}=\widehat{HAK}=\widehat{MKA}=90^0\)

\(\Rightarrow AKMH\) là hình chữ nhật

b) Do \(MK\perp AB\left(cmt\right)\)

Mà \(AB\perp AC\) (\(\Delta ABC\) vuông tại A)

\(\Rightarrow MK\) // \(AC\)

Mà \(M\) là trung điểm của BC

\(\Rightarrow K\) là trung điểm của AB

Tứ giác AMBI có:

K là trung điểm của AB (cmt)

K là trung điểm của MI (gt)

\(\Rightarrow AMBI\) là hình bình hành

\(\Rightarrow AI=BM\)

Mà \(BM=CM\) (do M là trung điểm của BC)

\(\Rightarrow AI=CM\)

Do \(AMBI\) là hình bình hành (cmt)

\(\Rightarrow AI\) // \(BM\)

\(\Rightarrow AI\) // \(CM\)

Tứ giác \(ACMI\) có:

\(AI\) // \(CM\left(cmt\right)\)

\(AI=CM\left(cmt\right)\)

\(\Rightarrow ACMI\) là hình bình hành

Mà E là trung điểm của AM

\(\Rightarrow\) E là trung điểm của CI

Hay C, E, I thẳng hàng

c) Để \(AKMH\) là hình vuông thì:

\(MH=MK\) (1)

Do \(MH\perp AC\) (cmt)

\(AC\perp AB\left(cmt\right)\)

\(\Rightarrow MH\) // \(AB\)

Mà M là trung điểm của BC

\(\Rightarrow H\) là trung điểm của AC

\(\Rightarrow MH\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow MH=\dfrac{AB}{2}\) (2)

Lại có:

M là trung điểm của BC (cmt)

K là trung điểm của AB (cmt)

\(\Rightarrow MK\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow MK=\dfrac{AC}{2}\) (3)

Từ (1), (2), (3) \(\Rightarrow AB=AC\)

\(\Rightarrow\Delta ABC\) cân tại A

Vậy để AKMH là hình vuông thì \(\Delta ABC\) vuông cân tại A

giúp em với ạ em cảm ơn

    (a+b+c)2$\ge$ 3(ab+bc+ca) (*)

=>a2+b2+c2+2ab+2bc+2ca$\ge$ 3ab+3bc+3ca

=>a2+b2+c2$\ge$ ab+bc+ca

nhân 2 vào cho 2 vế ta được:

2a2+2b2+2c2$\ge$ 2ab+2bc+2ca

=> (a+b)2+(b+c)2+(c+a)2$\ge$ 0 (đúng)

=> (*) đúng

 (a+b+c)^2 = a^2 + b^2 + c^2 + 2(ab+bc+ca) nha - HDT đặc biệt mở rộng

bắn tùm lum

Ta có: a2 + b2 + c2 = ab + bc + ca

2(a2 + b2 + c2) = 2(ab + bc + ca)

2a2 + 2b2 + 2c2 = 2ab + 2bc + 2ca

(a2 − 2ab + b2) + (b2 − 2bc + c2) + (c2 − 2ca + a2) = 0

(a − b)2 + (b − c)2 + (c − a)2 = 0

Mà (a − b)2 ≥ 0; (b − c)2 ≥ 0; (c − a)2 ≥ 0 nên suy ra