\(\dfrac{x}{2}=\dfrac{y}{3}\)  => x = \(\dfrac{2}{3}\) .y 

\(\dfrac{y}{4}=\dfrac{z}{5}\) => z = \(\dfrac{5}{4}\).y

thay x = \(\dfrac{2}{3}\).y và z = \(\dfrac{5}{4}\).y vào biểu thức x + 2y - z = 28 ta có:

\(\dfrac{2}{3}\)y + 2y - \(\dfrac{5}{4}\) y = 28

y.( \(\dfrac{2}{3}+2-\dfrac{5}{4}\)) = 28

y. \(\dfrac{17}{12}\) = 28

y = 28 : \(\dfrac{17}{12}\)

y = \(\dfrac{336}{17}\)

x = \(\dfrac{2}{3}\). \(\dfrac{336}{17}\)

x = \(\dfrac{224}{17}\)

z = \(\dfrac{5}{4}\) . \(\dfrac{336}{17}\)

z = \(\dfrac{420}{17}\)

vậy (x,y,z) = (\(\dfrac{224}{17}\); \(\dfrac{336}{17}\); \(\dfrac{420}{17}\))

Từ sau bạn viết đề cẩn thận hơn nhé.

a) Do AB = AC nên tam giác ABC là tam giác cân, do đó \(\widehat{ABC}=\widehat{ACB}\) (đpcm)

b) Xét hai tam giác AMB và AMC có:

AB = AC (giả thiết)

MB = MC (giả thiết)

AM chung

Suy ra \(\Delta AMB=\Delta AMC\) (c.c.c) (đpcm)

Mình gợi ý nhé

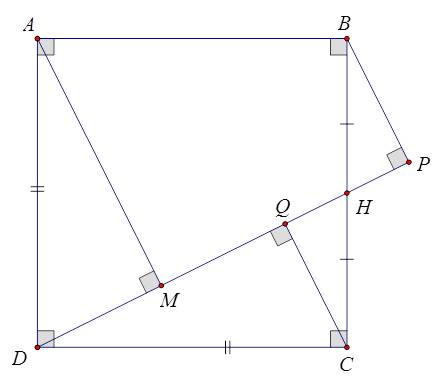
a) Hai tam giác vuông này có hai góc QHC và BHP bằng nhau (đối đỉnh); hai góc HQC và HPB bằng nhau (90^o) nên suy ra hai góc QCH và HBP cũng bằng nhau.

Từ đây chứng minh được \(\Delta QHC=\Delta PHB\left(g.c.g\right)\)

b) \(\widehat{DAM}=90^\circ-\widehat{ADM}=\widehat{QDC}=90^\circ-\widehat{QCD}=\widehat{QCH}\)

c) Từ câu b) suy ra \(\Delta DAM=\Delta CDQ\) (g.c.g) nên DM = CQ.

Ta có \(\widehat{A}=56^0;\widehat{B}=45^0\)

\(\Rightarrow\widehat{C}=180^0-\left(\widehat{A}+\widehat{B}\right)=180^0-\left(56^0+45^0\right)=79^0\)

Ta có \(\widehat{B}< \widehat{A}< \widehat{C}\Rightarrow AC< BC< AB\)  (quan hệ giữa cạnh và góc trong tam giác).

\(\text{Xét }\Delta ABC\text{ có:}\)

\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\left(\text{tính chất tổng ba góc một tam giác}\right)\)

\(\Rightarrow\widehat{C}=180^0-\left(\widehat{A}+\widehat{B}\right)\)

\(\Rightarrow\widehat{C}=180^0-\left(56^0+45^0\right)=79^0\)

\(\text{Xét }\Delta ABC\text{ có:}\)

\(\widehat{C}>\widehat{A}>\widehat{B}\left(79^0>56^0>45^0\right)\)

\(\Rightarrow AB>BC>AC\left(\text{quan hệ giữa góc và cạnh đối diện trong tam giác}\right)\)

toán nha ko phải tin nah  mọi người

\(\left|x-2021\right|=x-2021\)

\(\Leftrightarrow x-2021\ge0\)

\(\Leftrightarrow x\ge2021\)

Vậy nghiệm của pt là \(x\ge2021\)

Gọi biến của đa thức P cần tìm là x ta có

\(P=\left(x-2\right)\left(x-3\right)\left(x+4\right)=x^3-x^2-14x+24\)