bó 's tay

Gọi số ban đầu là \(\overline{ab}\)

Nếu đổi chỗ hàng chục và hàng đơn vị thì được một số mới lớn hơn số cũ 36 đơn vị nên \(\overline{ba}-\overline{ab}=36\)

=>10b+a-10a-b=36

=>-9a+9b=36

=>a-b=-4(1)

Chữ số hàng đơn vị hơn chữ số hàng chục là 4 đơn vị nên b-a=4

Do đó, ta có: b-a=4

=>b=a+4

=>\(\left(a;b\right)\in\left\{\left(1;5\right);\left(2;6\right);\left(3;7\right);\left(4;8\right);\left(5;9\right)\right\}\)

vậy: Các số cần tìm là 15;26;37;48;59

y = (m + 1) + 3

Hau y = (m + 1)\(x\) + 3 em ơi?

(m+1) x +3 ạ em lộn.

a: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)

Xét ΔBAC có BM là phân giác

nên \(\dfrac{AM}{AB}=\dfrac{CM}{BC}\)

=>\(\dfrac{AM}{12}=\dfrac{CM}{20}\)

=>\(\dfrac{AM}{3}=\dfrac{CM}{5}\)

mà AM+CM=AC=16cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AM}{3}=\dfrac{CM}{5}=\dfrac{AM+CM}{3+5}=\dfrac{16}{8}=2\)

=>\(AM=2\cdot3=6\left(cm\right);CM=2\cdot5=10\left(cm\right)\)

Xét ΔABC có MN//BC

nên \(\dfrac{MN}{BC}=\dfrac{AM}{AC}\)

=>\(\dfrac{MN}{20}=\dfrac{6}{16}=\dfrac{3}{8}\)

=>\(MN=20\cdot\dfrac{3}{8}=7,5\left(cm\right)\)

b: Xét ΔABC có MN//BC

nên \(\dfrac{CM}{MA}=\dfrac{BN}{NA}\)

mà \(\dfrac{CM}{MA}=\dfrac{BC}{BA}\)

nên \(\dfrac{BC}{BA}=\dfrac{BN}{NA}\)

\(\dfrac{AB}{AN}-\dfrac{BC}{AB}=\dfrac{AB}{AN}-\dfrac{BN}{AN}=\dfrac{AB-BN}{AN}=\dfrac{AN}{AN}=1\)

Điều kiện của $m$ để hàm số $y=(-2m+4)x+5$ là hàm số bậc nhất là $$m \neq 2$$.

a: Thay x=1 và y=2 vào y=(a-1)x+a, ta được:

1(a-1)+a=2

=>a-1+a=2

=>2a=3

=>\(a=\dfrac{3}{2}\)

b: Thay x=0 và y=-2 vào y=(a-1)x+a, ta được:

\(0\left(a-1\right)+a=-2\)

=>a=-2

c: Thay x=3 và y=0 vào y=(a-1)x+a, ta được:

3(a-1)+a=0

=>3a-3+a=0

=>4a=3

=>\(a=\dfrac{3}{4}\)

d: Để đường thẳng y=(a-1)x+a song song với đường thẳng y=2x+3 thì \(\left\{{}\begin{matrix}a-1=2\\a\ne3\end{matrix}\right.\)

=>\(a\in\varnothing\)

Cảm ơn bạn

a: Vì \(2\ne1\) nên (d1) cắt (d2)

b: Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}2x+1=x+1\\y=x+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-x=1-1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+1=1\end{matrix}\right.\)

Vậy: (d1) giao (d2) tại M(0;1)

c: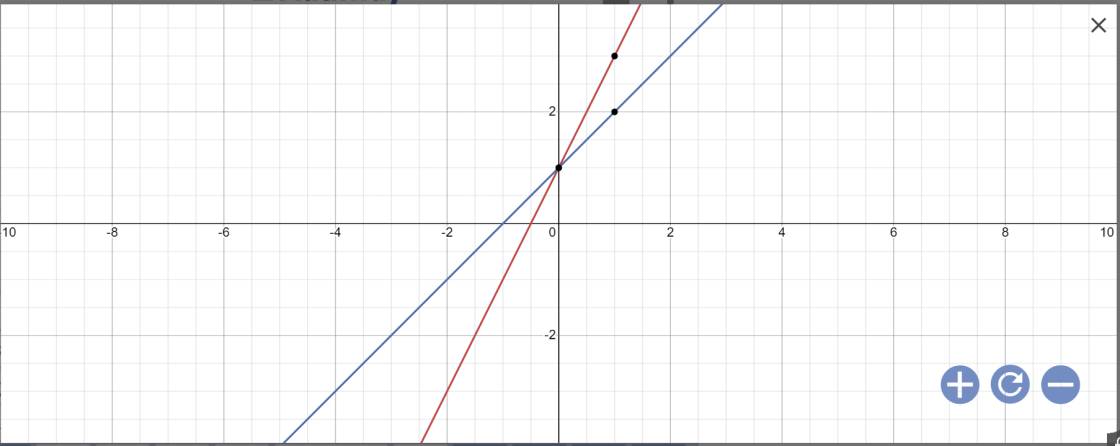 

d: Gọi A,B lần lượt là giao điểm của (d1),(d2) với trục Ox

Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-1\end{matrix}\right.\)

Vậy: M(0;1); A(-0,5;0); B(-1;0)

\(MA=\sqrt{\left(-0,5-0\right)^2+\left(0-1\right)^2}=\dfrac{\sqrt{5}}{2}\)

\(MB=\sqrt{\left(-1-0\right)^2+\left(0-1\right)^2}=\sqrt{2}\)

\(AB=\sqrt{\left(-1+0,5\right)^2+\left(0-0\right)^2}=0,5\)

Xét ΔMAB có \(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MV}=\dfrac{\dfrac{5}{4}+2-0,25}{2\cdot\dfrac{\sqrt{5}}{2}\cdot\sqrt{2}}=\dfrac{3}{\sqrt{10}}\)

=>\(sinAMB=\sqrt{1-\left(\dfrac{3}{\sqrt{10}}\right)^2}=\dfrac{1}{\sqrt{10}}\)

Diện tích tam giác AMB là:

\(S_{AMB}=\dfrac{1}{2}\cdot MA\cdot MB\cdot sinAMB\)

\(=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{10}}\cdot\dfrac{\sqrt{5}}{2}\cdot\sqrt{2}=\dfrac{1}{4}\)

Giúp mình đi mn

a: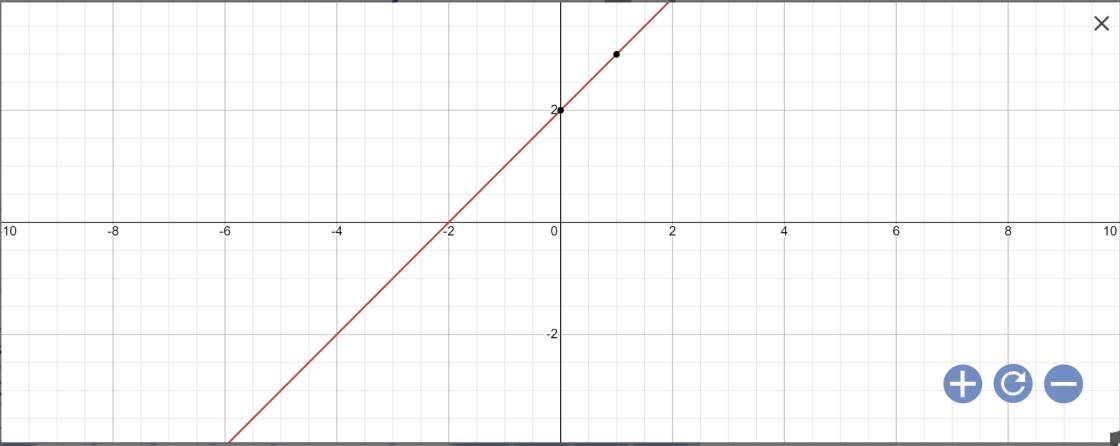 

b: Đặt (d'): y=ax+b

Vì (d')//(d) nên \(\left\{{}\begin{matrix}a=1\\b\ne2\end{matrix}\right.\)

Vậy: (d'): y=x+b

Thay x=3 và y=1 vào (d'), ta được:

b+3=1

=>b=-2

Vậy: (d'): y=x-2

c: y=3(m+1)x-3m-2

=(3m+3)x-3m-2

=3mx+3x-3m-2

=m(3x-3)+3x-2

Tọa độ điểm cố định mà đường thẳng y=3(m+1)x-3m-2 luôn đi qua là:

\(\left\{{}\begin{matrix}3x-3=0\\y=3x-2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=1\\y=3\cdot1-2=1\end{matrix}\right.\)

a) Do EF // AB nên theo định lý Thales ta có: IE/IA = FE/FB. 
--> Tương tự, do EF // CD nên IE/IC = IF/ID. 
=> Nhưng IA = IC và FB = ID (do I là giao điểm của 2 đường chéo trong hình thang) nên ta có IE = IF.
b) Do EF // AB và EF // CD nên theo định lý Thales ta có: EF/AB = IF/ID và EF/CD = IE/IA. 
--> Cộng hai vế lại ta được: EF/AB + EF/CD = IF/ID + IE/IA = 2 (do IE = IF theo câu a). 
=> Suy ra 2/EF = 1/AB + 1/CD.

8u